Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
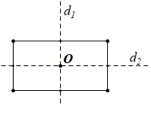
Tâm đối xứng \(O\) và các trục đối xứng \({d_1},{d_2}\) của hình chữ nhật đã cho được vẽ như hình dưới đây:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
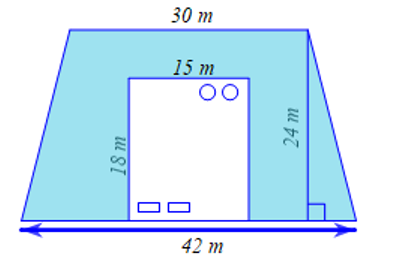
a) Diện tích khu đất làm nhà là: \(15.18 = 270\,\,\left( {{{\rm{m}}^2}} \right)\).
b) Diện tích khu đất hình thang cân dùng để làm nhà và trồng cỏ là:
\(\frac{1}{2}\left( {30 + 42} \right).24 = 864\,\,\left( {{{\rm{m}}^2}} \right)\)
Diện tích dùng để trồng cỏ là:
\(864 - 270 = 594\,\,\left( {{{\rm{m}}^2}} \right)\).
Để gieo hết bãi cỏ thì cần số túi hạt giống là:
\(594:33 = 18\) (túi).
Lời giải
Đặt \(A = 1 - 3 + {3^2} - {3^3} + ... + {\left( { - 3} \right)^x}\)
Khi đó \(3A = 3 - {3^2} + {3^3} - {3^4} + ... + {\left( { - 3} \right)^{x + 1}}\)
Suy ra \[A + 3A = \left[ {1 - 3 + {3^2} - {3^3} + ... + {{\left( { - 3} \right)}^x}} \right] + \left[ {3 - {3^2} + {3^3} - {3^4} + ... + {{\left( { - 3} \right)}^{x + 1}}} \right]\]
Do đó \(4A = 1 + {\left( { - 3} \right)^{x + 1}}\) nên \(A = \frac{{{{\left( { - 3} \right)}^{x + 1}} + 1}}{4}\)
Theo bài, \(A = 1 - 3 + {3^2} - {3^3} + ... + {\left( { - 3} \right)^x} = \frac{{{9^{1013}} + 1}}{4}\)
Suy ra \(\frac{{{{\left( { - 3} \right)}^{x + 1}} + 1}}{4} = \frac{{{9^{1013}} + 1}}{4}\)
Vì vậy \({\left( { - 3} \right)^{x + 1}} = {9^{1013}}\)
\({\left( { - 3} \right)^{x + 1}} = {3^{2026}}\)
\({\left( { - 3} \right)^{x + 1}} = {\left( { - 3} \right)^{2026}}\)
Suy ra \(x + 1 = 2026\), nên \(x = 2025\).
Vậy \(x = 2025\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(A = \left\{ {0;6;12;18;24;30} \right\}\);
B. \(A = \left\{ {6;12;18;24;30} \right\}\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.