Lúc 6 giờ 40 phút một xe ô tô đi liên tục từ A đến B với vận tốc 62,5 km/h thì đến B lúc 8 giờ 16 phút. Cùng lúc đó, có một xe máy cũng xuất phát từ A và đi liên tục về B với vận tốc bằng vận tốc của xe ô tô. Hỏi xe máy đến B lúc mấy giờ?
Lúc 6 giờ 40 phút một xe ô tô đi liên tục từ A đến B với vận tốc 62,5 km/h thì đến B lúc 8 giờ 16 phút. Cùng lúc đó, có một xe máy cũng xuất phát từ A và đi liên tục về B với vận tốc bằng vận tốc của xe ô tô. Hỏi xe máy đến B lúc mấy giờ?
Quảng cáo
Trả lời:
Thời gian để ô tô đi từ A đến B là:
8 giờ 16 phút ̶ 6 giờ 40 phút = 1 giờ 36 phút = 1,6 giờ
Quãng đường từ A đến B là: 62,5 × 1,6 = 100 (km)
Vận tốc của xe máy là: 62,5 × = 50 (km/h)
Thời gian để xe máy đi từ A đến B là: 100 : 50 = 2 (giờ)
Xe máy đến B lúc số giờ là: 6 giờ 40 phút + 2 giờ = 8 giờ 40 phút
Đáp số: 8 giờ 40 phút
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trung bình mỗi đội trồng được 13 510 cây, nên tổng số cây ba đội trồng được là:
13 510 × 3 = 40 530 (cây)
Vì số cây đội công nhân thứ nhất trồng bằng 40% tổng số cây đội công nhân thứ hai và đội công nhân thứ ba đã trồng, nên tỉ số giũa số cây đội thứ nhất với tổng số cây hai đội còn lại là:
Đưa về bài toán tổng – tỉ
Số cây đội công nhân thứ nhất trồng được là:
40 530 : (2 + 5) × 2 = 11 580 (cây)
Tổng số cây đội công nhân thứ hai và đội công nhân thứ ba đã trồng là:
40 530 ̶ 11 580 = 28950
Vì đội công nhân thứ hai trồng ít hơn đội công nhân thứ ba là 750 cây, nên hiệu giữa số cây đội công nhân thứ ba và đội thứ hai là: 750 (cây)
Đưa về bài toán tổng – hiệu
Số cây đội thứ hai trồng được là:
(28 950 ̶ 750) : 2 = 14 100 (cây)
Số cây đội thứ ba trồng được là:
28 950 ̶ 14 100 = 14 850 (cây)
Đáp số: đội thứ nhất: 11580 cây; đội thứ hai: 14 100 cây; đội thứ ba: 14 850 cây
Lời giải
a) Độ dài đáy lớn CD là: 10,5 × \(\frac{5}{3}\) = 17,5 (cm)
Độ dài chiều cao của hình thang là: 10,5 ̶ 1,3 = 9,2 (cm)
Diện tích hình thang ABCD là: (17,5 + 10,5) × 9,2 : 2 = 128,8 (cm2)
b)
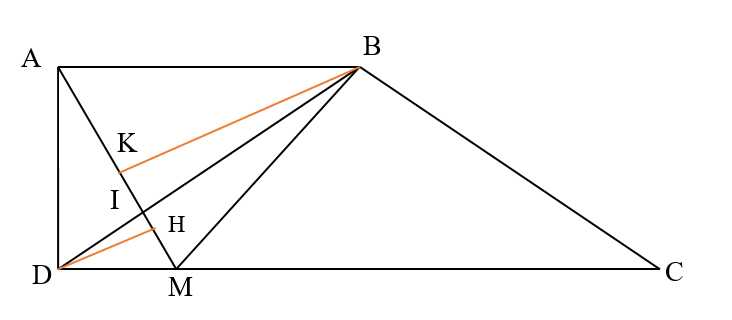
Vì MC = 4 MD và MC + MD = 17,5 nên
MC = 17,5 : (4 + 1) × 4 = 14 và MD = 17,5 ̶ 14 = 3,5
Tam giác ADI và tam giác ABI có cùng chiều cao hạ từ A và cạnh đáy lần lượt là ID và IB nên \(\frac{{{S_{ADI}}}}{{{S_{ABI}}}} = \frac{{ID}}{{IB}}\) (1)
Gọi H là chân đường cao hạ từ D xuống cạnh AM của tam giác ADM, khi đó DH cũng là chiều cao của tam giác ADI hạ từ D
Gọi K là chân đường cao hạ từ B xuống AM của tam giác ABM, khi đó BK cũng là chiều cao của tam giác ABI
Tam giác ADI và tam giác ABI có cùng cạnh đáy AI và hai chiều cao tương ứng là DH và BK nên \(\frac{{{S_{ADI}}}}{{{S_{ABI}}}} = \frac{{DH}}{{BK}}\) (2)
Tam giác ADM và tam giác ABM có cùng cạnh đáy AM nên \(\frac{{{S_{ADM}}}}{{{S_{ABM}}}} = \frac{{DH}}{{BK}}\) (3)
Mặt khác tam giác ADM có chiều cao AD bằng với chiều cao của tam giác ABM hạ từ M nên \(\frac{{{S_{ADM}}}}{{{S_{ABM}}}} = \frac{{DM}}{{BA}} = \frac{{3,5}}{{10,5}} = \frac{1}{3}\) (4)
Từ (1), (2), (3), (4) ta có \(\frac{{ID}}{{IB}} = \frac{1}{3}\)
Đáp số: a) 128,8 cm2
b) \(\frac{1}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Thửa ruộng thứ nhất
B. Thửa ruộng thứ hai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.