Vào năm 2025, các nhà khảo cổ học đã phát hiện ta một bản đồ kho báu tại Dubai (điểm \(D).\) Sau khi phân tích, họ đã chỉ các nơi được đánh dấu trên bản đồ tương ứng với những địa điểm sau: Thành phố Ajax (Điểm \(A\)), thủ đô Berlin (Điểm \(B\)), thủ độ Edinburgh (Điểm \(E\)), thành phố Chicago (Điểm \(C\)) và nơi chứa kho báu (điểm \(G\)). Các chuyên gia cho rằng, để tới được vị trí kho báu thì cần phải xuất phát từ Dubai (điểm \(D\)). Tất nhiên, chỉ có thể chọn một tuyến đường duy nhất trong những tuyến đường được dự đoán dưới đây để dẫn đến kho báu.
Tuyến đường 1: \(D \to A \to B \to E \to G\).
Tuyến đường 2: \(D \to A \to B \to C \to G\).
Tuyến đường 3: \(D \to C \to G\).
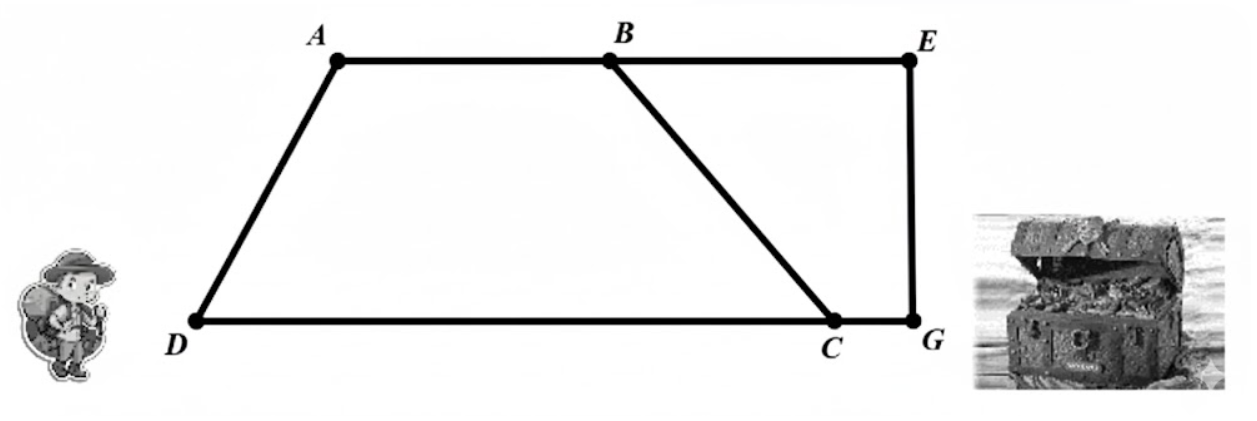
Sau khi tính toán kĩ khoảng cách giữa các địa điểm, nhà phân tích thu được kết quả như sau:
Quãng đường
\(DA\)
\(AB\)
\(BE\)
\(EG\)
\(BC\)
\(DC\)
\(CG\)
Độ dài
(km)
6
5
5
5
6
10
2
Em hãy cho biếu trong ba tuyến đường trên thì tuyến đường nào nhanh nhất để dẫn tới kho báu? Tính độ dài quãng đường đó.
Vào năm 2025, các nhà khảo cổ học đã phát hiện ta một bản đồ kho báu tại Dubai (điểm \(D).\) Sau khi phân tích, họ đã chỉ các nơi được đánh dấu trên bản đồ tương ứng với những địa điểm sau: Thành phố Ajax (Điểm \(A\)), thủ đô Berlin (Điểm \(B\)), thủ độ Edinburgh (Điểm \(E\)), thành phố Chicago (Điểm \(C\)) và nơi chứa kho báu (điểm \(G\)). Các chuyên gia cho rằng, để tới được vị trí kho báu thì cần phải xuất phát từ Dubai (điểm \(D\)). Tất nhiên, chỉ có thể chọn một tuyến đường duy nhất trong những tuyến đường được dự đoán dưới đây để dẫn đến kho báu.
Tuyến đường 1: \(D \to A \to B \to E \to G\).
Tuyến đường 2: \(D \to A \to B \to C \to G\).
Tuyến đường 3: \(D \to C \to G\).

Sau khi tính toán kĩ khoảng cách giữa các địa điểm, nhà phân tích thu được kết quả như sau:
|
Quãng đường |
\(DA\) |
\(AB\) |
\(BE\) |
\(EG\) |
\(BC\) |
\(DC\) |
\(CG\) |
|
Độ dài (km) |
6 |
5 |
5 |
5 |
6 |
10 |
2 |
Em hãy cho biếu trong ba tuyến đường trên thì tuyến đường nào nhanh nhất để dẫn tới kho báu? Tính độ dài quãng đường đó.
Quảng cáo
Trả lời:
Hướng dẫn giải
Độ dài tuyến đường 1 là: \(DA + AB + BE + EG = 6 + 5 + 5 + 5 = 21\,\,\left( {{\rm{km}}} \right)\).
Độ dài tuyến đường 2 là: \(DA + AB + BC + CG = 6 + 5 + 6 + 2 = 19\,\,\left( {{\rm{km}}} \right)\)
Độ dài tuyến đường 3 là: \(DC + CG = 10 + 2 = 12\,\,\left( {{\rm{km}}} \right)\).
Do đó, tuyến đường 3 là tuyến đi tới kho báu nhanh nhất là tuyến đường 3 với độ dài 12 km.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
Ta có \[\frac{{2025}}{1} = 2025 = \underbrace {1 + 1 + 1... + 1}_{2025\,\,so\,\,hang}\]
Khi đó:
\(B = \frac{{2025}}{1} + \frac{{2024}}{2} + \frac{{2013}}{3} + \ldots + \frac{1}{{2025}}\)
\( = 1 + \left( {\frac{{2024}}{2} + 1} \right) + \left( {\frac{{2013}}{3} + 1} \right) + \ldots + \left( {\frac{1}{{2025}} + 1} \right)\)
\( = 1 + \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}}\)
\( = \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}} + \frac{{2026}}{{2026}}\)
\(B = 2026 \cdot \left( {\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{2025}} + \frac{1}{{2026}}} \right) = 2026A\)
Ta có \(\frac{B}{A} = \frac{{2026A}}{A} = 2026.\)
Vậy \(\frac{B}{A} = 2026.\)
Lời giải
Hướng dẫn giải
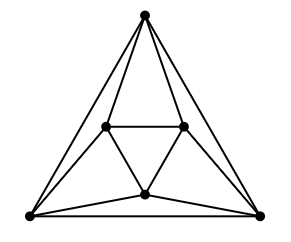
Học sinh vẽ đúng sơ đồ mắc vòng như sau:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.