Làm thế nào để chia đều 11 cái bánh nướng cùng loại, có kích thước và khối lượng như nhau cho 12 người sao cho không cái bánh nào phải chia thành quá 10 phần?
Làm thế nào để chia đều 11 cái bánh nướng cùng loại, có kích thước và khối lượng như nhau cho 12 người sao cho không cái bánh nào phải chia thành quá 10 phần?
Quảng cáo
Trả lời:
Hướng dẫn giải
Lấy 6 cái bánh, mỗi cái chia làm đôi được 12 phần bằng nhau, mỗi người được một phần là \(\frac{1}{2}\) cái bánh.
Lấy 3 cái bánh, mỗi cái chia đều làm 4 phần được 12 phần bằng nhau, mỗi người được một phần là \(\frac{1}{4}\) cái bánh.
Lấy 2 cái bánh cuối cùng, mỗi cái chia đều thành 6 phần được 12 phần bằng nhau, mỗi người được một phần là \(\frac{1}{6}\) cái bánh.
Như vậy, mỗi người được ba phần bánh, tổng cộng là: \(\frac{1}{2} + \frac{1}{4} + \frac{1}{6} = \frac{{11}}{{12}}\) (cái bánh).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
Ta có \[\frac{{2025}}{1} = 2025 = \underbrace {1 + 1 + 1... + 1}_{2025\,\,so\,\,hang}\]
Khi đó:
\(B = \frac{{2025}}{1} + \frac{{2024}}{2} + \frac{{2013}}{3} + \ldots + \frac{1}{{2025}}\)
\( = 1 + \left( {\frac{{2024}}{2} + 1} \right) + \left( {\frac{{2013}}{3} + 1} \right) + \ldots + \left( {\frac{1}{{2025}} + 1} \right)\)
\( = 1 + \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}}\)
\( = \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}} + \frac{{2026}}{{2026}}\)
\(B = 2026 \cdot \left( {\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{2025}} + \frac{1}{{2026}}} \right) = 2026A\)
Ta có \(\frac{B}{A} = \frac{{2026A}}{A} = 2026.\)
Vậy \(\frac{B}{A} = 2026.\)
Lời giải
Hướng dẫn giải
Học sinh vẽ đúng sơ đồ mắc vòng như sau:
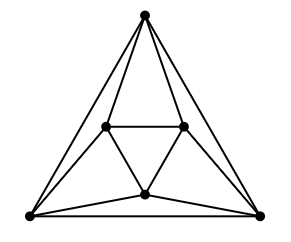
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.