Một ô tô muốn đi từ địa điểm A đến địa điểm C, nhưng giữa A và C là một ngọn núi cao nên ô tô phải đi thành 2 đoạn từ A lên B (ô tô leo dốc lên núi) và từ B đến C (ô tô xuống núi). Các đoạn đường tạo thành tam giác ABC với AB = 15km, BC = 20km và \[\widehat {ABC} = 135^\circ \]. Biết rằng cứ chạy 1km, ô tô tiêu thụ hết 0,5 lít xăng. Giá xăng RON 95 hiện nay là 24842 đồng/lít. Nếu người ta đào một đường hầm xuyên qua núi chạy thẳng từ \(A\) đến \(C\) thì ô tô chạy trên con đường mới này tiết kiệm được bao nhiêu tiền xăng?(Kết quả được làm tròn đến hàng nghìn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
+) Khi chưa có đường hầm:
Quãng đường ô tô đi từ A đến C là: \[15 + 20 = 35\](km)
Số lít xăng tiêu thụ: \[35 \cdot 0,5 = 17,5\](lít)
+) Khi có đường hầm:
Quãng đường ô tô đi từ A đến C là:
\[AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC\cos 135^\circ } \]
\[ = \sqrt {{{15}^2} + {{20}^2} - 2.15.20.\cos 135^\circ } \]
\[ \simeq 32,4\]
Số lít xăng tiêu thụ: \[32,4 \cdot 0,5 = 16,2\](lít)
+) Số lít xăng tiết kiệm được là: \[17,5--16,2{\rm{ }} = 1,3\](lít)
Số tiền tiết kiệm được là: \(1,3 \cdot 24\,\,842 \approx 32000\) đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
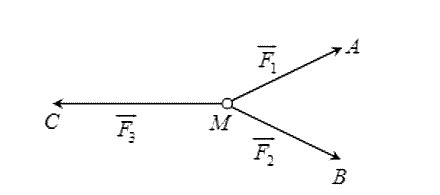
Vì vật đứng yên nên \(\overrightarrow {{F_{12}}} + \overrightarrow {{F_3}} = 0\)\( \Rightarrow \overrightarrow {{F_{12}}} = - \overrightarrow {{F_3}} \) do đó \(\overrightarrow {{F_{12}}} = \overrightarrow {{F_3}} \)
Mà tam giác \(MAB\) đều nên \({F_3} = 100\sqrt 3 \) (N).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Vẽ đường thẳng d : \[2x - y = 3.\]
Thay \(O\left( {0;\,0} \right)\) vào d ta thấy \(0 \le 3\) (vô lí)
Do đó miền nghiệm là nửa mặt phẳng d chứa điểm \[O\] và kể cả đường thẳng d.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} .\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập