Đọc đoạn trích sau và trả lời câu hỏi:
Dốc lên khúc khuỷu, dốc thăm thẳm
Heo hút cồn mây súng ngửi trời
Ngàn thước lên cao, ngàn thước xuống
Nhà ai Pha Luông mưa xa khơi.
Anh bạn dãi dầu không bước nữa
Gục lên súng mũ bỏ quên đời!
(Tây Tiến, Quang Dũng)
Biện pháp nghệ thuật nhân hoá trong đoạn trích trên thể hiện nét riêng nào trong vẻ đẹp tâm hồn của người lính Tây Tiến?
Quảng cáo
Trả lời:
Đáp án đúng là B
Phương pháp giải
Căn cứ vào nội dung văn bản, kiến thức về biện pháp nghệ thuật.
Nội dung/ Thông điệp
Lời giải
- Thứ nhất, cần xác định hình ảnh sử dụng biện pháp nghệ thuật nhân hoá là “súng ngửi trời”.
- Nghĩa thực có thể hiểu là súng chạm đến bầu trời (vì con đường hành quân đến những điểm cao, thậm chí là đỉnh đồi, đỉnh núi). Xét về tác dụng của biện pháp nghệ thuật, câu thơ trở nên hóm hỉnh, tinh nghịch, thể hiện được vẻ hào hoa của những chàng lính xuất thân từ tầng lớp trí thức Hà thành. -> Thể hiện vẻ đẹp lạc quan, hóm hỉnh của người lính Tây Tiến.
- Đặt trong hoàn cảnh những người lính đang hành quân vất vả, họ không hề nghĩ đến sự mệt mỏi, vất vả trên con đường gập ghềnh đã qua hay cả cuộc chiến trước mắt; trong một khoảnh khắc đặt trên lên những đỉnh núi, đỉnh đồi, họ bắt gặp đầu súng chạm đến bầu trời. Nhưng thay vì sử dụng từ “chạm” hay “đến”, tác giả lựa chọn từ “ngửi” để thể hiện đúng nét hồn nhiên, lạc quan có chút tếu táo, dí dỏm, hóm hỉnh của những chàng lính có xuất thân từ tầng lớp trí thức Hà thành. Đó chính là nét riêng của những người lính Hà thành.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "34"
Phương pháp giải
Vận dụng công thức tính lực điện.
Vận dụng kiến thức động lực học để xác định các lực tác dụng.
Áp dụng công thức tính quãng đường.
Lời giải
Chọn chiều dương là chiều chuyển động của (e), bỏ qua tác dụng của trọng lực nên:
\( - {F_d} = m{a_1} \Leftrightarrow - |q|E = m{a_1} \Leftrightarrow - \frac{{|q|U}}{{md}} = - 1,{6.10^{14}}\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)
Quãng đường (e) đi được kể từ t = 0 đến khi dừng lại lần đầu tiên là: \({s_1} = - \frac{{v_0^2}}{{2{a_1}}} = 3,{2.10^{ - 2}}\,(\;{\rm{m}})\)
Thời gian chuyển động của (e ) ứng với quãng đường s1 là: \({t_1} = \frac{{ - {v_0}}}{{{a_1}}} = {20.10^{ - 9}}(s)\)
Sau khi dừng lại, (e ) sẽ chuyển động nhanh dần đều ngược chiều đường sức với gia tốc:
\({a_2} = - {a_1} = 1,{6.10^{14}}\,\,\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\)
khoảng thời gian chuyển động còn lại là: \({t_2} = t - {t_1} = {5.10^{ - 9}}(\;{\rm{s}})\)
Quãng đường đi được trong khoảng thời gian t2 là: \(\frac{{{a_2}.t_2^2}}{2} = {2.10^{ - 3}}\;{\rm{m}}\)
Tổng quãng đường mà (e) đi được là: \(S = {s_1} + {s_2} = 3,{4.10^{ - 2}}(\;{\rm{m}}) = 3,4(\;{\rm{cm}}) = 34\;{\rm{mm}}\)
Lời giải
Đáp án đúng là C
Phương pháp giải
Số điểm cực trị của \(y = |f(x)| = \) Số điểm cực trị của \(y = f(x) + \) Số nghiệm bội lẻ của \(f(x) = 0\).
Lời giải
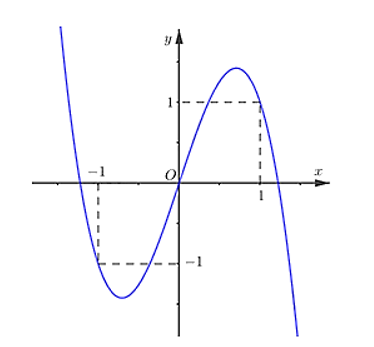
Xét \(g(x) = f(x) - \frac{{{x^2}}}{2} \Rightarrow {g^\prime }(x) = {f^\prime }(x) - x\).
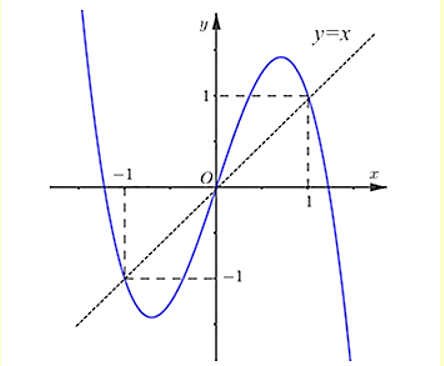
Từ đồ thị ta thấy: \({g^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{x = - 1}\end{array}} \right.\)
Vì hệ số cao nhất của \(f(x)\) nhỏ hơn 0 nên hệ số cao nhất của \(g(x)\) cùng nhỏ hơn 0. Ta có bảng biến thiên:
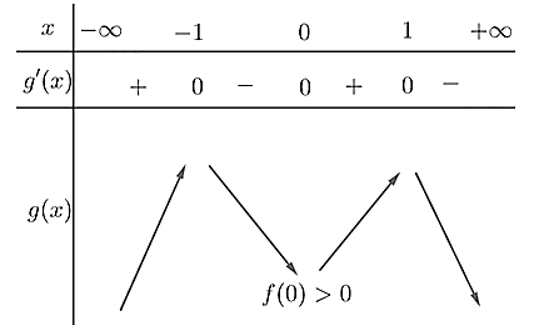
\( \Rightarrow g(x) = 0\) luôn có đúng 2 nghiệm bội lé.
Số điểm cực trị của hàm số \(y = \left| {f(x) - \frac{{{x^2}}}{2}} \right|\) là 5 .
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.