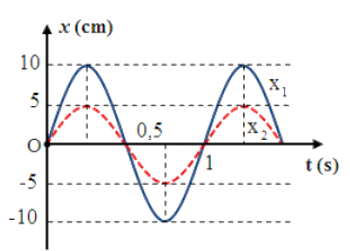
Có hai con lắc lò xo giống nhau đều có khối lượng vật nhỏ là m. Mốc thế năng tại vị trí cân bằng và π² ≈ 10. X₁, X₂ lần lượt là đồ thị ly độ theo thời gian của con lắc thứ nhất và thứ hai như hình vẽ. Tại thời điểm t con lắc thứ nhất có động năng 0,06J và con lắc thứ hai có thế năng 0,005J .Giá trị của khối lượng m(g) là

Đáp án:  ____

 

Đáp án đúng là A

Phương pháp giải

Áp dụng công thức: \({v^2} - v_0^2 = 2as\)

Sử dụng kết hợp định luật II và III Newton.

Lời giải

Sau khi 2 vật rời nhau và giao tốc cùng như nhau nên ta có gia tốc chuyển động của hai vật là:

\(a = \frac{{0 - v_1^2}}{{2{s_1}}} = \frac{{0 - v_2^2}}{{2{s_2}}}\)

\( \Rightarrow \frac{{{v_1}}}{{{v_2}}} = \sqrt {\frac{{{s_1}}}{{{s_2}}}} \)

Áp dụng định luật III Newton ta có: \(\overrightarrow {{F_{21}}} = - \overrightarrow {{F_{12}}} \Rightarrow {m_1}{a_1} = {m_2}{a_2}\)

\( \Rightarrow \frac{{{m_1}}}{{{m_2}}} = \frac{{{a_2}}}{{{a_1}}} = \frac{{{v_2}}}{{{v_1}}} = \sqrt {\frac{{{s_1}}}{{{s_2}}}} \)

\( \Rightarrow \frac{{{s_1}}}{{{s_2}}} = {\left( {\frac{{{m_1}}}{{{m_2}}}} \right)^2} = \frac{1}{4}\)

Đáp án đúng là "34"

Phương pháp giải

Vận dụng công thức tính lực điện.

Vận dụng kiến thức động lực học để xác định các lực tác dụng.

Áp dụng công thức tính quãng đường.

Lời giải

Chọn chiều dương là chiều chuyển động của (e), bỏ qua tác dụng của trọng lực nên:

\( - {F_d} = m{a_1} \Leftrightarrow  - |q|E = m{a_1} \Leftrightarrow  - \frac{{|q|U}}{{md}} =  - 1,{6.10^{14}}\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)

Quãng đường (e) đi được kể từ t = 0 đến khi dừng lại lần đầu tiên là: \({s_1} =  - \frac{{v_0^2}}{{2{a_1}}} = 3,{2.10^{ - 2}}\,(\;{\rm{m}})\)

Thời gian chuyển động của (e ) ứng với quãng đường s₁ là: \({t_1} = \frac{{ - {v_0}}}{{{a_1}}} = {20.10^{ - 9}}(s)\)

Sau khi dừng lại, (e ) sẽ chuyển động nhanh dần đều ngược chiều đường sức với gia tốc:

\({a_2} =  - {a_1} = 1,{6.10^{14}}\,\,\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\)

khoảng thời gian chuyển động còn lại là: \({t_2} = t - {t_1} = {5.10^{ - 9}}(\;{\rm{s}})\)

Quãng đường đi được trong khoảng thời gian t₂ là: \(\frac{{{a_2}.t_2^2}}{2} = {2.10^{ - 3}}\;{\rm{m}}\)

Tổng quãng đường mà (e) đi được là: \(S = {s_1} + {s_2} = 3,{4.10^{ - 2}}(\;{\rm{m}}) = 3,4(\;{\rm{cm}}) = 34\;{\rm{mm}}\)