Một máy tạo rung được sử dụng để tạo ra sóng trên dây.
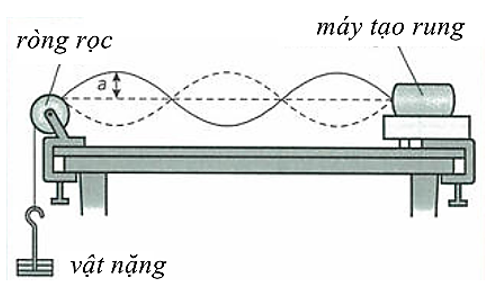
Từ hình vẽ ta thấy trên dây có:
Một máy tạo rung được sử dụng để tạo ra sóng trên dây.

Từ hình vẽ ta thấy trên dây có:
B. 4 bụng và 3 nút sóng
Quảng cáo
Trả lời:
Đáp án đúng là C
Phương pháp giải
Quan sát hình vẽ.
Vận dụng lí thuyết về sóng dừng.
Lời giải
Từ đồ thị ta thấy trên dây đang có sóng dừng với 3 bụng sóng và 4 nút sóng.
Câu hỏi cùng đoạn
Câu 2:
Cho khoảng cách từ ròng rọc đến máy tạo rung là 90cm. Bước sóng của sóng trên là:
Đáp án đúng là B
Phương pháp giải
Sử dụng điều kiện có sóng dừng trên dây với hai đầu cố định: \(l = k\frac{\lambda }{2}\)
Lời giải
Điều kiện có sóng dừng trên dây với hai đầu định: \(l = k\frac{\lambda }{2}\)
Ta thấy trên dây có 3 bụng sóng \( \Rightarrow 90 = 3.\frac{\lambda }{2} \Rightarrow \lambda = 60\;{\rm{cm}}\)
Câu 3:
Tần số của máy tạo rung là 60Hz. Khi đó, vận tốc sóng truyền truyên dây là:
Tần số của máy tạo rung là 60Hz. Khi đó, vận tốc sóng truyền truyên dây là:
Đáp án đúng là B
Phương pháp giải
Áp dụng công thức: v=λf
Lời giải
Áp dụng công thức tính vận tốc truyền sóng:
v = λf = 60.60 = 3600cm/s = 36m/s
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "34"
Phương pháp giải
Vận dụng công thức tính lực điện.
Vận dụng kiến thức động lực học để xác định các lực tác dụng.
Áp dụng công thức tính quãng đường.
Lời giải
Chọn chiều dương là chiều chuyển động của (e), bỏ qua tác dụng của trọng lực nên:
\( - {F_d} = m{a_1} \Leftrightarrow - |q|E = m{a_1} \Leftrightarrow - \frac{{|q|U}}{{md}} = - 1,{6.10^{14}}\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)
Quãng đường (e) đi được kể từ t = 0 đến khi dừng lại lần đầu tiên là: \({s_1} = - \frac{{v_0^2}}{{2{a_1}}} = 3,{2.10^{ - 2}}\,(\;{\rm{m}})\)
Thời gian chuyển động của (e ) ứng với quãng đường s1 là: \({t_1} = \frac{{ - {v_0}}}{{{a_1}}} = {20.10^{ - 9}}(s)\)
Sau khi dừng lại, (e ) sẽ chuyển động nhanh dần đều ngược chiều đường sức với gia tốc:
\({a_2} = - {a_1} = 1,{6.10^{14}}\,\,\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\)
khoảng thời gian chuyển động còn lại là: \({t_2} = t - {t_1} = {5.10^{ - 9}}(\;{\rm{s}})\)
Quãng đường đi được trong khoảng thời gian t2 là: \(\frac{{{a_2}.t_2^2}}{2} = {2.10^{ - 3}}\;{\rm{m}}\)
Tổng quãng đường mà (e) đi được là: \(S = {s_1} + {s_2} = 3,{4.10^{ - 2}}(\;{\rm{m}}) = 3,4(\;{\rm{cm}}) = 34\;{\rm{mm}}\)
Lời giải
Đáp án đúng là C
Phương pháp giải
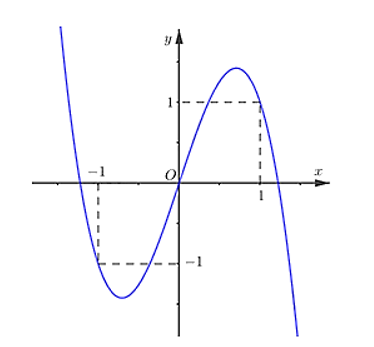
Số điểm cực trị của \(y = |f(x)| = \) Số điểm cực trị của \(y = f(x) + \) Số nghiệm bội lẻ của \(f(x) = 0\).
Lời giải
Xét \(g(x) = f(x) - \frac{{{x^2}}}{2} \Rightarrow {g^\prime }(x) = {f^\prime }(x) - x\).
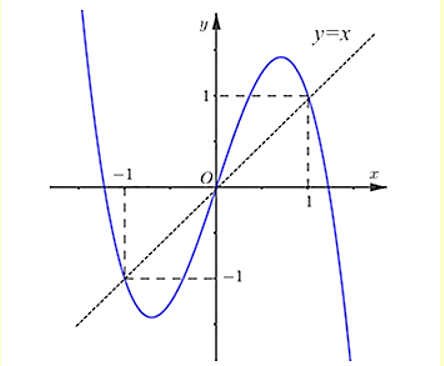
Từ đồ thị ta thấy: \({g^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{x = - 1}\end{array}} \right.\)
Vì hệ số cao nhất của \(f(x)\) nhỏ hơn 0 nên hệ số cao nhất của \(g(x)\) cùng nhỏ hơn 0. Ta có bảng biến thiên:
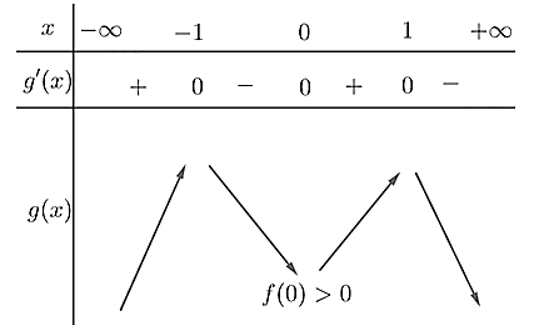
\( \Rightarrow g(x) = 0\) luôn có đúng 2 nghiệm bội lé.
Số điểm cực trị của hàm số \(y = \left| {f(x) - \frac{{{x^2}}}{2}} \right|\) là 5 .
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.