Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm M, N, P lần lượt là trung điểm các cạnh SA, BC, CD. Gọi I, J lần lượt là giao điểm của NP với AB, AD. Kéo dài MI cắt SB tại \(E\), kéo dài MJ cắt SD tại \(E\). Gọi \(k = \frac{{EF}}{{IJ}}\), giá trị của \(k\) là?
Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm M, N, P lần lượt là trung điểm các cạnh SA, BC, CD. Gọi I, J lần lượt là giao điểm của NP với AB, AD. Kéo dài MI cắt SB tại \(E\), kéo dài MJ cắt SD tại \(E\). Gọi \(k = \frac{{EF}}{{IJ}}\), giá trị của \(k\) là?
A. \(k = \frac{2}{3}\)
B. \(k = \frac{1}{9}\)
C. \(k = \frac{1}{3}\)
D. \(k = \frac{2}{9}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là D
Phương pháp giải
Chứng minh: ΔBNI∼ΔCNP để suy ra tỉ lệ bằng nhau. Áp dụng định lý Menelaus
Lời giải
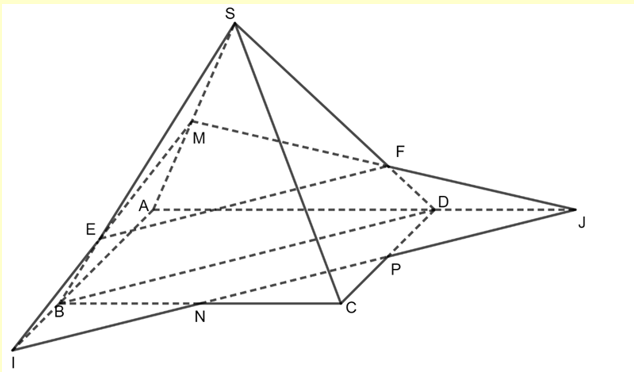
Vì N, P lần lượt là trung điểm \(BC,CD \Rightarrow NP\) là đường trung bình của tam giác BCD
hay
Xét \(\Delta BNI\) và \(\Delta CNP\) có: \(\left\{ {\begin{array}{*{20}{l}}{\widehat {IBN} = \widehat {NCP}}\\{\widehat {BNI} = \widehat {CNP}}\end{array}} \right.\)
\( \Rightarrow \Delta BNI\~\Delta CNP(g - g)\)
\( \Rightarrow \frac{{BN}}{{CN}} = \frac{{NI}}{{NP}} = \frac{{BI}}{{CP}} = 1\) (Vì N là trung điểm BC)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{NI = NP}\\{BI = CP}\end{array} \Rightarrow BI = \frac{1}{2}AB} \right.\) hay \(IB = \frac{1}{3}AI\)
Áp dụng định lý Menelaus trong \(\Delta SAB\) ta có: \(\frac{{MS}}{{MA}}.\frac{{IA}}{{IB}}.\frac{{EB}}{{ES}} = 1\)
\( \Rightarrow \frac{{IA}}{{IB}}.\frac{{EB}}{{ES}} = 1\)
Mà \(IB = \frac{1}{3}AI \Rightarrow 3.\frac{{EB}}{{ES}} = 1 \Rightarrow \frac{{EB}}{{ES}} = \frac{1}{3}\)
Chứng minh tương tự ta có \(\frac{{FD}}{{FS}} = \frac{1}{3}\)
Xét tam giác SBD có \(:\frac{{EB}}{{ES}} = \frac{{FD}}{{FS}} = \frac{1}{3}\)
Theo định lý Thales và \(EF = \frac{1}{3}BD\)
Xét \(\Delta AIJ\) có
\( \Rightarrow BD = \frac{2}{3}IJ\)
Vậy \(EF = \frac{1}{3}.\frac{2}{3}IJ = \frac{2}{9}IJ\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là B
Phương pháp giải
+ Tính ab/ab -> ab = ?
+ Tính f khi biết ab
=> Tính tỉ lệ các kiểu hình còn lại
Ruồi giấm đực không có HVG
Lời giải
Ruồi cái thân đen, cánh cụt, mắt đỏ:
\(A - bb{X^D}{X^ - } = 10,25\% \Rightarrow A - bb = \frac{{0,1025}}{{0,5{X^D}{X^ - }}} = 0,205\)
\( \Rightarrow \frac{{ab}}{{ab}} = 0,045 \to \underline {ab} \)♀\( = 0,09 = \frac{f}{2}\)(vì bên đực không có HVG nên cho ab = 0,5)
⇒ tần số HVG = 18% ⇒ A−B− = 0,545
I đúng, số kiểu gene tối đa: 7 × 4 = 28; số kiểu hình = 4 × 3= 12.
II sai, tần số HVG = 18%.
III sai, A-B-XDY = 0,545 0,25 XDY = 0,13625.
IV đúng, số cá thể cái dị hợp tử về 1 trong 3 cặp gene:
(0,41Ab + 0,41aB) × (0,5AB + 0,5ab) × 0,25XDXD + (0,09AB × 0,5AB + 0,09ab × 0,5ab) × 0,25XDXd = 0,2275
Câu 2
A. 10Pa.
B. 104Pa.
C. 10N/m2.
D. 5.103Pa.
Lời giải
Đáp án đúng là D
Phương pháp giải
Áp suất phân tử chất khí: \(p = \frac{1}{3}\rho \overline {{v^2}} \)
Lời giải
Áp suất mà khí đó tác dụng lên thành bình là:
\(p = \frac{1}{3}.\frac{m}{V}\overline {{v^2}} = \frac{1}{3}\rho \overline {{v^2}} \)
\[ \to p = \frac{1}{3}{.6.10^{ - 2}}{.500^2} = {5.10^3}\,(Pa)\]
Câu 3
A. Phát huy vai trò của nhân dân trong chiến tranh bảo vệ Tổ quốc.
B. Sự ủng hộ của lực lượng dân chủ, yêu chuộng hòa bình thế giới.
C. Được sự ủng hộ tích cực của các nước xã hội chủ nghĩa.
D. Sự lãnh đạo của Mặt trận Liên hiệp quốc dân Việt Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Đất nước tạm thời bị chia cắt.
B. Miền Bắc hoàn thành công nghiệp hóa.
C. Xu thế toàn cầu hóa xuất hiện.
D. Cuộc Chiến tranh lạnh đã kết thúc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Δt2 = 0,50C; Δt3 = 1,60C.
B. Δt2 = 0,50C; Δt3 = 1,70C.
C. Δt2 = 0,40C; Δt3 = 1,70C
D. Δt2 = 0,40C; Δt3 = 1,60C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Chiến dịch thể hiện được đường lối kháng chiến chống thực dân Pháp.
B. Chiến dịch thắng lợi góp phần quyết định việc kết thúc chiến tranh.
C. Bộ đội chủ lực thi đấu tên được thể được chiến thuật định điểm.
D. Quân đội Việt Nam đánh bại một kế hoạch quân sự của thực dân Pháp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tạo thời cơ chín muồi đấu tranh giải phóng dân tộc.
B. Cổ vũ các dân tộc đứng lên đấu tranh giành độc lập.
C. Thúc đẩy các dân tộc đa phương hoá quan hệ ngoại giao.
D. Đánh dấu sự sụp đổ hoàn toàn của chủ nghĩa đế quốc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập