Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng B,H,C). Gọi P, Q lần lượt là chân đường vuông góc kẻ từ M đến AB, AC.
a) Chứng minh MP + MQ = AH
b) Gọi K là trung điểm của AM. Chứng minh rằng KH \( \bot \) PQ
c) Cho đường tròn (O) nội tiếp tam giác ABM. Gọi D,E,F theo thứ tự là tiếp điểm của (O) với các cạnh BM,AB,AM. Vẽ DN vuông góc với EF tại N. Chứng minh \(\widehat {BNE} = \widehat {MNF}\)
Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng B,H,C). Gọi P, Q lần lượt là chân đường vuông góc kẻ từ M đến AB, AC.
a) Chứng minh MP + MQ = AH
b) Gọi K là trung điểm của AM. Chứng minh rằng KH \( \bot \) PQ
c) Cho đường tròn (O) nội tiếp tam giác ABM. Gọi D,E,F theo thứ tự là tiếp điểm của (O) với các cạnh BM,AB,AM. Vẽ DN vuông góc với EF tại N. Chứng minh \(\widehat {BNE} = \widehat {MNF}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
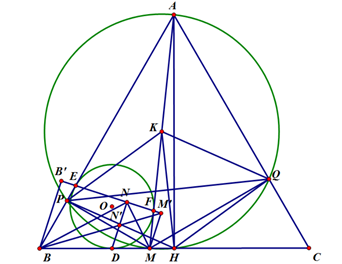
a) Trong \(\Delta \)BMP vuông ở P. ta có: \(MP = MB.\sin MBP = MB.sin60^\circ = \frac{{\sqrt 3 }}{2}MB\)
Tương tự, ta chứng minh được: \(MQ = \frac{{\sqrt 3 }}{2}MC\)
Vậy \(MP + MQ = \frac{{\sqrt 3 }}{2}BC = AH\)
b) Do \(\widehat {APM} = \widehat {AQM} = \widehat {AHM}\) = 90 ° nên A, M, P, Q, H cùng nằm trên đường tròn đường kính AM. Do đó, K là tâm của đường tròn này\( \Rightarrow \) KP = KH = KQ
Trong \(\Delta \) PKH cân ở K có \(\widehat {PHK} = \widehat {2PAH} = 2\widehat {BAH}\)=2. 30 °=\(60^\circ .\;\)Vậy \(\Delta \) PKH đều \( \Rightarrow HP = HK\;\left( 1 \right)\)
Tương tự, là chứng minh được \(\Delta \)QKH đều \( \Rightarrow \;HQ = HK\;\left( 2 \right)\)
Từ (1), (2) ta được:
\(\left. {\begin{array}{*{20}{c}}{HQ = HK}\\{M\`a \;PQ = PK}\end{array}} \right\} \Rightarrow PQ\) là đường trung trực của \(HK \Rightarrow PQ \bot HK\)
c) Gọi B', M' lần lượt là hình chiếu của B, M lên EF. Khi đó do BB'||DN||MM' Gọi N là giao điểm của DN và BM.
Áp dụng định lý Thales trong \(\Delta \) BMM'; \(\Delta \) M'BB' có BB'||DN|| MM'; D \( \in BM;N' \in BM';N \in B'M',\;\) ta có:
\(\left. {\begin{array}{*{20}{c}}{\frac{{MD}}{{DB}} = \frac{{M'N'}}{{N'B}}}\\{\frac{{M'N'}}{{N'B}} = \frac{{M'N}}{{NB'}}}\end{array}} \right\} \Rightarrow \frac{{BD}}{{DM}} = \frac{{B'N}}{{NM'}}\;\left( 3 \right)\)
Xét \(\Delta \)BB'E và \(\Delta \) MM'F , ta có:
\(\widehat {BB'E} = \widehat {MM'F} = 90^\circ \)
\(\widehat {BEB'} = \widehat {AEF} = \widehat {AFE}\) (\(\Delta \;AEF\;\)cân tại F do AE = AF theo tính chất tiếp tuyến )
\( = \widehat {MFM'}\)
Vậy \(\Delta \;BB'E\;\~\;\Delta \;\;MM'F\;\left( {g.g} \right) \Rightarrow \frac{{B'E}}{{M'F}} = \frac{{BE}}{{MF}} = \frac{{BD}}{{DM}}\;\)(4) ( do \(BE = BD\;;MF = MD\;\)theo tính chất tiếp tuyến )
Từ (3) và (4 ), ta được \(\frac{{B'M}}{{NM'}} = \frac{{B'E}}{{M'F}} = \frac{{B'N - B'E}}{{\;NM' - M'F}} = \frac{{EN}}{{FN}}\)
Xét \(\Delta \;BNE\;v\`a \;\Delta \;MNF,\;ta\;c\'o :\)
\(\widehat {BEN} = \widehat {MFN}\)
\(\frac{{EN}}{{FN}} = \frac{{B'N}}{{MN'}} = \frac{{BE}}{{MF}}\;\left( {CMT} \right)\)
Vậy
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta áp dụng tính chất a - S (a) \( \vdots \) 9 với mọi số nguyên dương a (bạn đọc tự chứng minh tính chất này)
Vậy ( a + b - S(a) = a + b - S(a+b)\( \vdots \)9
\( \Rightarrow \left( {a - S\left( a \right)} \right) + b \vdots 9 \Rightarrow b \vdots 9\)
Tương tự , ta được \(a \vdots 9.\) Vậy a , b chia hết cho 9 (đpcm)
b) Phương trình viết lại:
\(2{x^2} + 2x + 1 = 2{y^4} + 4{y^3} + 6{y^2} + 4y + 1\)
\( \Rightarrow 2{x^2} + 2x + 2 = 2{y^4} + 4{y^3} + 6{y^2} + 4y + 2\;\)
\(\;\;\;\; \Rightarrow {x^2} + x + 1 = {\left( {{y^2} + y + 1} \right)^2}\)
Vậy từ đây ta được \({x^2} + x + 1\) là số chính phương hay \(4{x^2} + 4x + 4 = {\left( {2x + 1} \right)^2} + 3\;\)là số chính phương.
Đặt (**)
Ta có:
\(\left( {**} \right) \Leftrightarrow {t^2} - {\left( {2x + 1} \right)^2} = 3\)
\( \Leftrightarrow \left( {t - 2x - 1} \right)\left( {t + 2x + 1} \right) = 3\)
Xét tất cả các trường hợp sau:
|
\(t - 2x - 1\) |
1 |
3 |
-1 |
-3 |
|
\(t + 2x + 1\) |
3 |
1 |
-3 |
-1 |
|
\(t\) |
2 |
2 |
-2 |
-2 |
|
\(x\) |
0 |
-1 |
-1 |
0 |
Vậy \(x = 0\;v\`a \;x = - 1\)
Với x = 0 thay vào (*), ta được:
(*)\( \Leftrightarrow {\left( {{y^2} + y + 1} \right)^2} = 1\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{y^2} + y + 1 = 1 \Leftrightarrow {y^2} + y = 0 \Leftrightarrow y\left( {y + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{y = 0}\\{y = - 1}\end{array}} \right.}\\{{y^2} + y + 1 = - 1\left( {v\^o \;nghiem} \right)}\end{array}} \right.\)
Với x = - 1 thay vào (*), ta được:
(*)\(\; \Leftrightarrow {\left( {{y^2} + y + 1} \right)^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{y = 0}\\{y = - 1}\end{array}} \right.\)
Vậy phương trình có các nghiệm (x; y) = (0; 0); (0; - 1); (- 1; 0); (- 1; - 1)
Lời giải
Ta gọi ô (i; j) là ô ở dòng thứ i và cột thứ j trong bảng. Khi đó, sau tất cả các thao tác đổi dấu, ô (i; j) bị đổi dấu i +5j+1 (lần) và i + 5j +1 \( \equiv \) i+j+1 (mod 2)
Sau tất cả các thao tác đổi dấu, ô (\(i\);\(j\) ) sẽ mang “ + ”nếu bị dỗi dấu một số chẵn lần. Vậy sau khi thao tác, các ô (i; j) mang dấu “ + ” và chỉ khi i + j + 1 j + 1\( \vdots \;\)2 hay i, j khác tính chẵn lė.
Th 1 : i lẽ, j chẵn.
Ta chọn i thỏa mãn thì có 12 cách, chọn j thỏa thì có 11 cách. Vậy số ô (i; j) thỏa thì là 12.11 =132( ô )
Th2: i chẵn, j lẻ.
Bằng cách chọn tương tự, ta được só ô thỏa mãn là 11.12 =132 (ô)
Vậy số ô mang dấu “ + ” sau khi thự hiện đổi dấu 132 + 132 = 246 ô
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập