Chia bảng hình vuông có cạnh 23cm thành các ô vuông có cạnh bằng 1cm. Ban đầu, tất cả các ô vuông được điền bởi dấu "+". Sau đó người ta thực hiện đổi dấu (mỗi lần đổi dấu là chuyển " + " thành " — ", " — " thành “ + “ ) trong các ô vuông ở các dòng và các cột của bảng theo quy tắc sau:

·        Tất cả các ô của dòng thứ i được đổi dấu i lần (\(i \in N\;,\;1 \le i \le 23\) )

·        Tất cả các ô ở cột thứ j được đổi dấu 5j + 1 lần (\(j \in N\;,\;1 \le j \le 23\) )

     Hỏi sau khi thực hiện tất cả thao tác đổi dấu, trên bảng còn bao nhiêu dấu " + "?

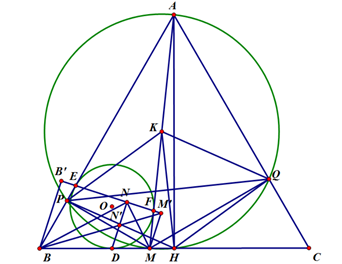
a) Trong \(\Delta \)BMP vuông ở P. ta có: \(MP = MB.\sin MBP = MB.sin60^\circ = \frac{{\sqrt 3 }}{2}MB\)

               Tương tự, ta chứng minh được: \(MQ = \frac{{\sqrt 3 }}{2}MC\)

               Vậy \(MP + MQ = \frac{{\sqrt 3 }}{2}BC = AH\)

            b) Do \(\widehat {APM} = \widehat {AQM} = \widehat {AHM}\) = 90 ° nên A, M, P, Q, H cùng nằm trên đường  tròn đường kính AM. Do đó, K là tâm của đường tròn này\( \Rightarrow \) KP = KH = KQ

              Trong \(\Delta \) PKH cân ở K có \(\widehat {PHK} = \widehat {2PAH} = 2\widehat {BAH}\)=2. 30 °=\(60^\circ .\;\)Vậy \(\Delta \) PKH đều \( \Rightarrow HP = HK\;\left( 1 \right)\)

              Tương tự, là chứng minh được \(\Delta \)QKH đều \( \Rightarrow \;HQ = HK\;\left( 2 \right)\)

               Từ (1), (2) ta được:

                     \(\left. {\begin{array}{*{20}{c}}{HQ = HK}\\{M\`a \;PQ = PK}\end{array}} \right\} \Rightarrow PQ\) là đường trung trực của \(HK \Rightarrow PQ \bot HK\)

         c) Gọi B', M' lần lượt là hình chiếu của B, M lên EF. Khi đó do BB'||DN||MM' Gọi N là giao điểm của DN và BM.

             Áp dụng định lý Thales trong \(\Delta \) BMM'; \(\Delta \) M'BB' có BB'||DN|| MM'; D \( \in BM;N' \in BM';N \in B'M',\;\) ta có:

                                 \(\left. {\begin{array}{*{20}{c}}{\frac{{MD}}{{DB}} = \frac{{M'N'}}{{N'B}}}\\{\frac{{M'N'}}{{N'B}} = \frac{{M'N}}{{NB'}}}\end{array}} \right\} \Rightarrow \frac{{BD}}{{DM}} = \frac{{B'N}}{{NM'}}\;\left( 3 \right)\)

             Xét \(\Delta \)BB'E và \(\Delta \) MM'F , ta có:

                   \(\widehat {BB'E} = \widehat {MM'F} = 90^\circ \)

                   \(\widehat {BEB'} = \widehat {AEF} = \widehat {AFE}\) (\(\Delta \;AEF\;\)cân tại F do AE = AF theo tính chất tiếp tuyến )

                                          \( = \widehat {MFM'}\)

                   Vậy \(\Delta \;BB'E\;\~\;\Delta \;\;MM'F\;\left( {g.g} \right) \Rightarrow \frac{{B'E}}{{M'F}} = \frac{{BE}}{{MF}} = \frac{{BD}}{{DM}}\;\)(4) ( do \(BE = BD\;;MF = MD\;\)theo tính chất tiếp tuyến )

                  Từ (3) và (4 ), ta được \(\frac{{B'M}}{{NM'}} = \frac{{B'E}}{{M'F}} = \frac{{B'N - B'E}}{{\;NM' - M'F}} = \frac{{EN}}{{FN}}\)

                  Xét \(\Delta \;BNE\;v\`a \;\Delta \;MNF,\;ta\;c\'o :\)

                             \(\widehat {BEN} = \widehat {MFN}\)

                            \(\frac{{EN}}{{FN}} = \frac{{B'N}}{{MN'}} = \frac{{BE}}{{MF}}\;\left( {CMT} \right)\)

                   Vậy $\Delta BNE ~ \Delta MNF \left(c.g.c\right)\Rightarrow \widehat{BNE}=\widehat{MNF}\left(ĐPCM\right)$