1. Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\), điểm \(E\) thuộc cung nhỏ của đường tròn \(\left( O \right)\,\,\left( {E \ne A,\,E \ne B} \right)\). Đường thẳng \(AE\) cắt các tiếp tuyến tại \(B,\,C\)của đường tròn \(\left( O \right)\) lần lượt tại \(M,\,N\).
a) Chứng minh rằng \(MB.NC = A{B^2}\).
b) Gọi \(F\) là giao điểm của \(MC\) và \(BN\), \(H\) là trung điểm \(BC\). Chứng minh rằng ba điểm \(E,\,F,\,H\) thẳng hàng.
2. Cho đường tròn \(\left( O \right)\) và hai điểm \(A,\,B\) cố định nằm trên đường tròn \(\left( O \right)\) sao cho \(\widehat {AOB} = {120^0}\). Điểm \(M\) thay đổi trên cung lớn của đường tròn \(\left( O \right)\). Đường tròn nội tiếp tam giác \(MAB\) tiếp xúc với \(MA,\,MB\) lần lượt tại \(E,\,F\). Chứng minh rằng đường thẳng \[EF\] luôn tiếp xúc với một đường tròn cố định.
Quảng cáo
Trả lời:
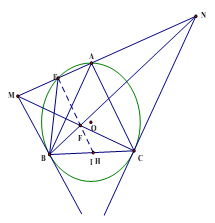
1)Ta có \(\widehat {ABM} = \widehat {ACB} = \widehat {BAC} = {60^0} \Rightarrow BM//AC \Rightarrow \widehat {BMA} = \widehat {CAN}\,\,\left( 1 \right)\)
Tương tự ta có \(CN//AB \Rightarrow \widehat {BAM} = \widehat {CNA}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(\Delta AMB\) đồng dạng \(\Delta NAC\) (g-g)
\( \Rightarrow \frac{{MB}}{{AC}} = \frac{{AB}}{{NC}} \Rightarrow MB.NC = AB.AC \Rightarrow MB.NC = A{B^2}\)
Gọi \(I\) là giao điểm của \[EF\] và \(BC\). Từ a) suy ra \(MB.NC = B{C^2} \Rightarrow \frac{{MB}}{{BC}} = \frac{{BC}}{{NC}}\,\,\,\left( 3 \right)\)
Mặt khác \(\widehat {MBC} = \widehat {MBA} + \widehat {ABC} = {60^0} + {60^0} = {120^0}\). Tương tự \(\widehat {BCN} = {120^0}\)
Suy ra \(\widehat {MBC} = \widehat {BCN}\,\left( 4 \right)\)
Từ (3) và (4) ta có \(\Delta MBC\) đồng dạng \(\Delta BCN\)(c-g-c). Suy ra \(\widehat {BMC} = \widehat {NBC}\)
Ta có \(\widehat {BFM} = \widehat {BCF} + \widehat {FBC} = \widehat {BCF} + \widehat {BMC} = {180^0} - \widehat {MBC} = {60^0}\,\left( 5 \right)\)
Do \(BEAC\)nội tiếp nên \(\widehat {BEM} = \widehat {BCA} = {60^0}\,\,\left( 6 \right)\)
Từ (5) và (6) ta có \(\widehat {BFM} = \widehat {BEM}\). Suy ra \(BMEF\) nội tiếp
\[\widehat {BEF} = \widehat {BMF} = \widehat {NBC} = \widehat {FBI}\]. Do đó \(\Delta IBF\) đồng dạng \(\Delta IEB\)(g-g). Suy ra \(\frac{{IB}}{{IE}} = \frac{{IF}}{{IB}} \Rightarrow I{B^2} = IE.IF\,\,\left( 7 \right)\)
Chứng minh tương tự ta có \(I{C^2} = IE.IF\,\,\left( 8 \right)\).
Từ (7) và (8) suy ra \(IB = IC \Rightarrow I \equiv H\). Vậy \(E,\,F,\,H\) thẳng hàng.
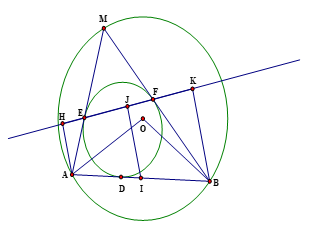
2)Gọi \(I\) là trung điểm của \(AB\). Vẽ \(AH,\,IJ,\,BK\) cùng vuông góc \(EF\).
Ta có \(\widehat {AOB} = {120^0} \Rightarrow \widehat {AMB} = {60^0}\), hơn nữa \(ME = \,MF\) nên tam giác \(MEF\) đều.
Tam giác vuông \(AHE\) có \(AH = AE.\sin \,{60^0} = \frac{{\sqrt 3 }}{2}.AE = \frac{{\sqrt 3 }}{2}.AD\,\,\,\left( 1 \right)\)
Tam giác vuông \(BKF\) có \(BK = BF.\sin \,{60^0} = \frac{{\sqrt 3 }}{2}BF = \frac{{\sqrt 3 }}{2}BD\,\,\left( 2 \right)\)
Cộng vế (1) và (2) ta có
\(AH + BK = \frac{{\sqrt 3 }}{2}AB \Rightarrow 2IJ = \frac{{\sqrt 3 }}{2}AB \Rightarrow IJ = \frac{{\sqrt 3 }}{4}AB\) không đổi.
Vì điểm \(I\) cố định nên \(EF\) tiếp xúc với đường tròn cố định tâm \(I\), bán kính \(\frac{{\sqrt 3 }}{4}AB\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1)Đặt \(A = 2{p^4} - {p^2} + 16\)
Với \(p = 3\) thì \(A = 169 = {13^2}\) là số chính phương. Vậy \(p = 3\) thoả mãn.
Với \(p > 3\) thì \({p^2} \equiv 1\left( {\bmod 3} \right)\). Suy ra\({p^4} = {\left( {{p^2}} \right)^2} \equiv 1\left( {\bmod 3} \right)\)
Suy ra \(A = 2{p^4} - {p^2} + 16 \equiv 2.1 - 1 + 16 \equiv 2\left( {\bmod 3} \right)\)
Do các số chính phương chia cho 3 chỉ dư \(0\) hoặc 1 nên \(A\) không là số chính phương.
2)Ta có phương trình
\(\begin{array}{l}6{x^2} + 7xy + 2{y^2} + x + y - 1 = 1\\ \Leftrightarrow 6{x^2} + \left( {7y + 1} \right)x + 2{y^2} + y - 1 = 1\\ \Leftrightarrow \left( {2x + y + 1} \right)\left( {3x + 2y - 1} \right) = 1\end{array}\)
\(\left[ \begin{array}{l}\left\{ \begin{array}{l}2x + y + 1 = 1\\3x + 2y - 1 = 1\end{array} \right.\,\,\,\,\left( 1 \right)\\\left\{ \begin{array}{l}2x + y + 1 = - 1\\3x + 2y - 1 = - 1\end{array} \right.\,\,\,\,\left( 2 \right)\end{array} \right.\)
\(\left( 1 \right) \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 4\end{array} \right.\)
\(\left( 2 \right) \Leftrightarrow \left\{ \begin{array}{l}x = - 4\\y = 6\end{array} \right.\)
Lời giải
1)Ta có: \({a^2} + {b^2} + 2 = {\left( {a + b} \right)^2}\)
Nên
\(\begin{array}{l}Q = \frac{1}{{{{\left( {a + b} \right)}^3}}}\left( {\frac{1}{{{a^3}}} + \frac{1}{{{b^3}}}} \right) + \frac{3}{{{{\left( {a + b} \right)}^4}}}\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}}} \right) + \frac{6}{{{{\left( {a + b} \right)}^4}}}\\ = \frac{{{a^3} + {b^3}}}{{{{\left( {a + b} \right)}^3}}} + \frac{{3\left( {{a^2} + {b^2}} \right)}}{{{{\left( {a + b} \right)}^4}}} + \frac{6}{{{{\left( {a + b} \right)}^4}}}\\ = \frac{{\left( {{a^3} + {b^3}} \right)\left( {a + b} \right) + 3\left( {{a^2} + {b^2}} \right) + 6}}{{{{\left( {a + b} \right)}^4}}}\end{array}\)
\(\begin{array}{l} = \frac{{{a^4} + {b^4} + ab\left( {{a^2} + {b^2}} \right) + 3\left( {{a^2} + {b^2}} \right) + 6}}{{{{\left( {{a^2} + {b^2} + 2} \right)}^2}}}\\ = \frac{{{a^4} + {b^4} + 4\left( {{a^2} + {b^2}} \right) + 6}}{{{{\left( {{a^2} + {b^2} + 2} \right)}^2}}}\end{array}\)
\[\begin{array}{l} = \frac{{\left( {{a^4} + {b^4} + 2{a^2}{b^2}} \right) + 4\left( {{a^2} + {b^2}} \right) + 4}}{{{{\left( {{a^2} + {b^2} + 2} \right)}^2}}}\\ = \frac{{{{\left( {{a^2} + {b^2}} \right)}^2} + 4\left( {{a^2} + {b^2}} \right) + 4}}{{{{\left( {{a^2} + {b^2} + 2} \right)}^2}}}\end{array}\]
\[\begin{array}{l} = \frac{{{{\left( {{a^2} + {b^2} + 2} \right)}^2}}}{{{{\left( {{a^2} + {b^2} + 2} \right)}^2}}}\\ = 1\end{array}\]
2)\(P = \sqrt {{x^2} + 1} \sqrt {{y^2} + 1} + xy - \left( {x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} } \right) = \sqrt {{x^2} + 1} \sqrt {{y^2} + 1} + xy - \sqrt {15} \)
Đặt \(\begin{array}{l}M = \sqrt {{x^2} + 1} \sqrt {{y^2} + 1} + xy \Rightarrow {M^2} = \left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) + {x^2}{y^2} + 2xy\sqrt {{x^2} + 1} .\sqrt {{y^2} + 1} \\ = 2{x^2}{y^2} + {x^2} + {y^2} + 1 + 2xy\sqrt {{x^2} + 1} .\sqrt {{y^2} + 1} \end{array}\)
\(\begin{array}{l} = {x^2}\left( {{y^2} + 1} \right) + {y^2}\left( {{x^2} + 1} \right) + 2x\sqrt {{y^2} + 1} .y\sqrt {{x^2} + 1} + 1\\ = {\left( {x\sqrt {{y^2} + 1} + y\sqrt {{x^2} + 1} } \right)^2} + 1\end{array}\)
\( = 16 \Rightarrow M = 4\). Vậy \(P = 4 - \sqrt {15} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.