1. 1. Cho ba số thực dương \[a,{\rm{ }}b,{\rm{ }}c\] thoả mãn \[ab + bc + ca = 1\]. Tìm giá trị lớn nhất của biểu thức: P = \[\frac{{2a}}{{\sqrt {1 + {a^2}} }} + \frac{b}{{\sqrt {1 + {b^2}} }} + \frac{c}{{\sqrt {1 + {c^2}} }}\]
2. 2.Cho ba số thực không âm \(a,\;b,\;c\) thoả mãn \(ab + bc + ca + abc \le 4\). Chứng minh rằng \(a + b + c \ge ab + bc + ca.\)
1. 1. Cho ba số thực dương \[a,{\rm{ }}b,{\rm{ }}c\] thoả mãn \[ab + bc + ca = 1\]. Tìm giá trị lớn nhất của biểu thức: P = \[\frac{{2a}}{{\sqrt {1 + {a^2}} }} + \frac{b}{{\sqrt {1 + {b^2}} }} + \frac{c}{{\sqrt {1 + {c^2}} }}\]
2. 2.Cho ba số thực không âm \(a,\;b,\;c\) thoả mãn \(ab + bc + ca + abc \le 4\). Chứng minh rằng \(a + b + c \ge ab + bc + ca.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Ta có:
\(P = \frac{{2a}}{{\sqrt {1 + {a^2}} }} + \frac{b}{{\sqrt {1 + {b^2}} }} + \frac{c}{{\sqrt {1 + {c^2}} }}\)
\( = \frac{{2a}}{{\sqrt {{a^2} + ab + bc + ca} }} + \frac{b}{{\sqrt {{a^2} + ab + bc + ca} }} + \frac{c}{{\sqrt {{a^2} + ab + bc + ca} }}\)
\( = \frac{{2a}}{{\sqrt {\left( {a + b} \right)\left( {a + c} \right)} }} + \frac{b}{{\sqrt {\left( {b + c} \right)\left( {b + a} \right)} }} + \frac{c}{{\sqrt {\left( {c + a} \right)\left( {c + b} \right)} }}\)
\( = \sqrt {\frac{{2a}}{{a + b}}.\frac{{2a}}{{a + c}}} + \sqrt {\frac{{2b}}{{b + a}}.\frac{b}{{2\left( {b + c} \right)}}} + \sqrt {\frac{{2c}}{{c + a}}.\frac{c}{{2\left( {c + b} \right)}}} \)
\(AM - GM\)
\( \le \frac{1}{2}\left[ {\frac{{2a}}{{a + b}} + \frac{{2a}}{{a + c}} + \frac{{2b}}{{b + a}} + \frac{b}{{2\left( {b + c} \right)}} + \frac{{2c}}{{c + a}} + \frac{c}{{2\left( {c + b} \right)}}} \right]\)
\( = \frac{1}{2}\left[ {\left( {\frac{{2a}}{{a + b}} + \frac{{2b}}{{a + b}}} \right) + \left( {\frac{{2a}}{{a + c}} + \frac{{2a}}{{a + c}}} \right) + \frac{1}{2}\left( {\frac{b}{{b + c}} + \frac{c}{{b + c}}} \right)} \right]\;\)
\( = \frac{1}{2}\left( {2 + 2 + \frac{1}{2}} \right) = \frac{9}{4}\)
Dấu “=” xảy ra khi \(a = \frac{{7\sqrt {15} }}{{15}};b = c = \frac{{\sqrt {15} }}{{15}}\)
Vậy P đạt GTLN là \(\frac{9}{4}\) khi \(a = \frac{{7\sqrt {15} }}{{15}};b = c = \frac{{\sqrt {15} }}{{15}}\)2. Ta có \(ab + bc + ca + abc \le 4\)
\( \Leftrightarrow abc + 2\left( {ab + bc + ca} \right) + 4\left( {a + b + c} \right) + 8 \le \left( {ab + 2a + 2b + 4} \right) + \left( {bc + 2b + 2c + 4} \right)\)
\( + \left( {ca + 2c + 2a + 4} \right)\)
\( \Leftrightarrow \left( {a + 2} \right)\left( {b + 2} \right)\left( {c + 2} \right) \le \left( {a + 2} \right)\left( {b + 2} \right) + \left( {b + 2} \right)\left( {c + 2} \right)\)
\( + \left( {c + 2} \right)\left( {a + 2} \right)\)
\( \Leftrightarrow 1 \le \frac{1}{{a + 2}} + \frac{1}{{b + 2}} + \frac{1}{{c + 2}} \Leftrightarrow \frac{2}{{a + 2}} + \frac{2}{{b + 2}} + \frac{2}{{c + 2}}\;\; \ge 2\)
\( \Leftrightarrow \left( {1 - \frac{2}{{a + 2}}} \right) + \left( {1 - \frac{2}{{b + 2}}} \right) + \left( {1 - \frac{2}{{c + 2}}} \right) \le 1\)
\( \Leftrightarrow 1 \ge \frac{a}{{a + 2}} + \frac{b}{{b + 2}} + \frac{c}{{c + 2}}\)
Áp dụng BĐT Cauchy-Schwarz
\(1 \ge \frac{a}{{a + 2}} + \frac{b}{{b + 2}} + \frac{c}{{c + 2}} = \frac{{{a^2}}}{{{a^2} + 2a}} + \frac{{{b^2}}}{{{b^2} + 2b}} + \frac{{{c^2}}}{{{c^2} + 2c}}\)
\(C - S \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{{{a^2} + {b^2} + {c^2} + 2\left( {a + b + c} \right)}}\)
\( \Rightarrow {\left( {a + b + c} \right)^2} \le \left( {{a^2} + {b^2} + {c^2}} \right) + 2\left( {a + b + c} \right)\)
\( \Leftrightarrow a + b + c \ge ab + bc + ca\) (đpcm)Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
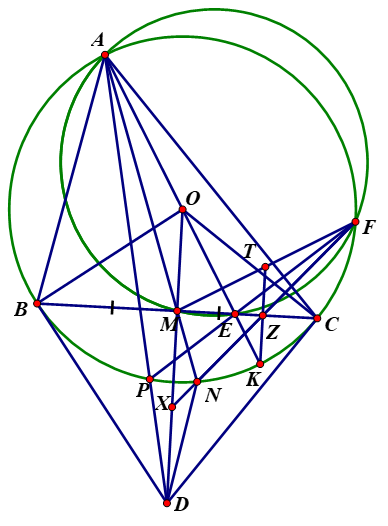
1. Xét đường tròn (O): \(BD \bot BO,\;CD \bot CO\) (tính chất tiếp tuyến)
\( \Rightarrow \widehat {DBO} = \widehat {DCO} = {90^\diamondsuit }\) \( \Rightarrow \widehat {DBO} + \widehat {DCO} = {180^\diamondsuit }\)
\( \Rightarrow \)Tứ giác OBDC nội tiếp
Lại có \(OB = OC,\;MB = MC,\;DB = DC\)
\( \Rightarrow O,\;M,\;D\) cùng thuộc trung trực của đoạn BC
Suy ra \(MO.MD = MB.MC\)
Mà tứ giác ABNC nội tiếp \( \Rightarrow MB.MC = MA.MN\)
\( \Rightarrow MO.MD = MA.MN\) \( \Rightarrow \) Tứ giác AOND nội tiếp
\( \Rightarrow DO\) là phân giác \(\widehat {ADN}\)b) Xét \({\rm{\Delta }}DBP\) và \({\rm{\Delta }}DAB\) có
\(\widehat {BDP}\;\)chung; \(\widehat {DBP} = \widehat {DAB}\)
\( \Rightarrow {\rm{\Delta }}DBP \sim {\rm{\Delta }}DAB\) (g.g) \( \Rightarrow \frac{{AB}}{{BP}} = \frac{{AD}}{{DB}}\)
Tương tự ta có \({\rm{\Delta }}DCP \sim {\rm{\Delta }}DAC \Rightarrow \frac{{AC}}{{CP}} = \frac{{AD}}{{DC}}\)
\( \Rightarrow \frac{{AB}}{{BP}} = \frac{{AC}}{{CP}} \Rightarrow AB.CP = AC.BP\)
Áp dụng định lý Ptoleney cho tứ giác ABPC nội tiếp ta có
\(AP.BC = AB:CP + AC.BP\)
\( \Rightarrow 2AP.CM = 2AC.BP \Rightarrow \frac{{AP}}{{AC}} = \frac{{BP}}{{CM}}\)
\({\rm{\Delta }}ABP\) và \({\rm{\Delta }}AMC\) có \(\frac{{AP}}{{AC}} = \frac{{BP}}{{CM}}\;;\;\widehat {APB} = \widehat {ACM}\)
\( \Rightarrow {\rm{\Delta }}ABP \sim {\rm{\Delta }}AMC\) (c.g.c) \( \Rightarrow \widehat {ABP} = \widehat {AMC}\)
Lại có tứ giác ABPF nội tiếp nên \(\widehat {ABP} = {180^\diamondsuit } - \widehat {AFP}\)
Lại có tứ giác AMEF nội tiếp nên \(\widehat {AME} = {180^\diamondsuit } - \widehat {AFB}\)
\( \Rightarrow \widehat {AFP} = \widehat {AFE} \Rightarrow E,\;F,\;P\) thẳng hàngc) Áp dụng hệ thức lượng cho \({\rm{\Delta }}OCD\) vuông tại C ta có
\(OM.OD = O{C^2} = O{F^2} \Rightarrow \frac{{OF}}{{OM}} = \frac{{OD}}{{OF}}\) \( \Rightarrow {\rm{\Delta }}OMF \sim {\rm{\Delta }}OFD\;\) (c.g.c)
\( \Rightarrow \widehat {OFD} = \widehat {OMF} = {90^\diamondsuit } - \widehat {CMF} = {90^\diamondsuit } - \widehat {FAE} = {90^\diamondsuit } - \widehat {AFO}\;\)
\( \Rightarrow AFD = {90^\diamondsuit } \Rightarrow AF \bot FD\) mà \(AF \bot FK\)
\( \Rightarrow DF = DK \Rightarrow D,\;F,\;K\) thẳng hàng
Gọi \(Z,\;X\) là giao \(FN\) với \(BC,\;DM\).
Gọi \(T\) là giao \(KZ\) với \(MF\).
Ta có \(D{C^2} = DK.DF = DM.DO \Rightarrow \) Tứ giác OMKF nội tiếp
\( \Rightarrow \widehat {KMF} = \widehat {KOF\;} = 2\widehat {OAF} = 2\widehat {FMS}\;\)
\( \Rightarrow \widehat {KME} = \widehat {FME} = \widehat {FAO} = \widehat {KNF}\) \( \Rightarrow \) Tứ giác MNKZ nội tiếp
\( \Rightarrow \widehat {KZM} = {180^\diamondsuit } - \widehat {MNK} = {90^\diamondsuit }\)
Lại có \({\rm{\Delta }}TMK\) có MZ là đường cao đồng thời là phân giác
\( \Rightarrow ZT = ZK\)
Do \(TK//DM \Rightarrow \frac{{ZT}}{{MX}} = \frac{{FZ}}{{FX}} = \frac{{ZK}}{{DX}}\)
\( \Rightarrow XD = XM \Rightarrow \) X là trung điểm của đoạn DM.
Vậy FN đi qua trung điểm của đoạn DMLời giải
Gọi \({a_1},\;{a_2},\; \ldots ,\;{a_{11}}\) lần lượt là số kẹo trong 11 gói.
Đặt \(S = {a_1} + {a_2} + \ldots + {a_{11}}\)
Giả sử tổn tại \(a \le k,\;l \le 11\;m\`a \;{a_k} \ne {a_l}\)
Theo bài ra, ta suy ra được \(S - {a_1},\;S - {a_2}, \ldots ,S - {a_{11}}\) đều là số chẵn
\( \Rightarrow {a_1},\;{a_2}, \ldots ,{a_{11}}\) cũng chẵn hoặc cũng lẻ
Ta thực hiện quá trình như sau:
· Nếu \({a_1},\;{a_2}, \ldots ,{a_{11}}\) cũng chẵn, ta thu được bộ số mới
\(\left( {{b_1},\;{b_2},\; \ldots ,\;{b_{11}}} \right) = \left( {\frac{{{a_1}}}{2},\frac{{{a_2}}}{2},\; \ldots ,\frac{{{a_{11}}}}{2}} \right)\)
· Nếu \({a_1},\;{a_2}, \ldots ,{a_{11}}\) cũng lẻ, ta thu được bộ số mới
\(\left( {{b_1},\;{b_2},\; \ldots ,\;{b_{11}}} \right) = \left( {\frac{{{a_1} - 1}}{2};\frac{{{a_2} - 1}}{2}; \ldots ;\frac{{{a_{11}} - 1}}{2}} \right)\)
Ta thấy 11 gói kẹo với số kẹo \({b_1};{b_2}; \ldots ;{b_{11}}\) cũng thoả mãn điều kiện đề bài.
Tiếp tục quá trình như vậy đến khi thu được bộ \(\left( {{x_1};{x_2}; \ldots ;{x_{11}}} \right)\) mà tồn tại \(1 \le j;i \le 11\) sao cho \(xj = 0;xi = 1\)
Mà bộ \(({z_1};{z_2}; \ldots ;{z_{11}})\) thoả mãn điều kiện đề bài nên \({x_1};{x_2}; \ldots ;{x_{11}}\) cùng tính chẵn lẻ (Mâu thuẫn)
Điều giả sử là sai.
Vậy \({a_1} = {a_2} = \ldots = {a_{11}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập