Sau khi tổ chức một trận đấu giao hữu giữa hai đội bóng lớp 9A và 9B, ban tổ chức có 11 gói kẹo muốn chia cho 2 đội. Mỗi đội được chia 5 gói làm phần thưởng và 1 gói ban tổ chức giữ lại để liên hoan. Biết rằng dù chọn bất kì gói nào để giữ lại, ban tổ chức luôn có thể chia 10 gói còn lại cho 2 đội mà tổng số viên kẹo trong 5 gói cho mỗi đội là bằng nhau. Chứng minh rằng 11 gói kẹo đó phải có số viên kẹo bằng nhau.
Sau khi tổ chức một trận đấu giao hữu giữa hai đội bóng lớp 9A và 9B, ban tổ chức có 11 gói kẹo muốn chia cho 2 đội. Mỗi đội được chia 5 gói làm phần thưởng và 1 gói ban tổ chức giữ lại để liên hoan. Biết rằng dù chọn bất kì gói nào để giữ lại, ban tổ chức luôn có thể chia 10 gói còn lại cho 2 đội mà tổng số viên kẹo trong 5 gói cho mỗi đội là bằng nhau. Chứng minh rằng 11 gói kẹo đó phải có số viên kẹo bằng nhau.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \({a_1},\;{a_2},\; \ldots ,\;{a_{11}}\) lần lượt là số kẹo trong 11 gói.
Đặt \(S = {a_1} + {a_2} + \ldots + {a_{11}}\)
Giả sử tổn tại \(a \le k,\;l \le 11\;m\`a \;{a_k} \ne {a_l}\)
Theo bài ra, ta suy ra được \(S - {a_1},\;S - {a_2}, \ldots ,S - {a_{11}}\) đều là số chẵn
\( \Rightarrow {a_1},\;{a_2}, \ldots ,{a_{11}}\) cũng chẵn hoặc cũng lẻ
Ta thực hiện quá trình như sau:
· Nếu \({a_1},\;{a_2}, \ldots ,{a_{11}}\) cũng chẵn, ta thu được bộ số mới
\(\left( {{b_1},\;{b_2},\; \ldots ,\;{b_{11}}} \right) = \left( {\frac{{{a_1}}}{2},\frac{{{a_2}}}{2},\; \ldots ,\frac{{{a_{11}}}}{2}} \right)\)
· Nếu \({a_1},\;{a_2}, \ldots ,{a_{11}}\) cũng lẻ, ta thu được bộ số mới
\(\left( {{b_1},\;{b_2},\; \ldots ,\;{b_{11}}} \right) = \left( {\frac{{{a_1} - 1}}{2};\frac{{{a_2} - 1}}{2}; \ldots ;\frac{{{a_{11}} - 1}}{2}} \right)\)
Ta thấy 11 gói kẹo với số kẹo \({b_1};{b_2}; \ldots ;{b_{11}}\) cũng thoả mãn điều kiện đề bài.
Tiếp tục quá trình như vậy đến khi thu được bộ \(\left( {{x_1};{x_2}; \ldots ;{x_{11}}} \right)\) mà tồn tại \(1 \le j;i \le 11\) sao cho \(xj = 0;xi = 1\)
Mà bộ \(({z_1};{z_2}; \ldots ;{z_{11}})\) thoả mãn điều kiện đề bài nên \({x_1};{x_2}; \ldots ;{x_{11}}\) cùng tính chẵn lẻ (Mâu thuẫn)
Điều giả sử là sai.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
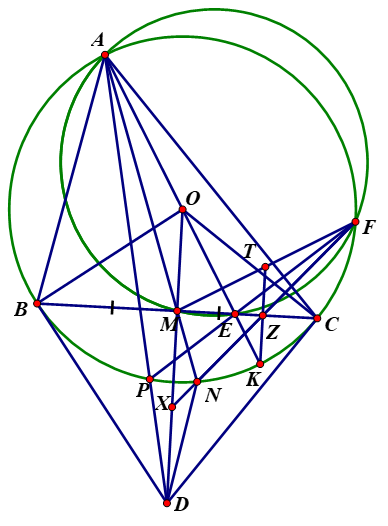
1. Xét đường tròn (O): \(BD \bot BO,\;CD \bot CO\) (tính chất tiếp tuyến)
\( \Rightarrow \widehat {DBO} = \widehat {DCO} = {90^\diamondsuit }\) \( \Rightarrow \widehat {DBO} + \widehat {DCO} = {180^\diamondsuit }\)
\( \Rightarrow \)Tứ giác OBDC nội tiếp
Lại có \(OB = OC,\;MB = MC,\;DB = DC\)
\( \Rightarrow O,\;M,\;D\) cùng thuộc trung trực của đoạn BC
Suy ra \(MO.MD = MB.MC\)
Mà tứ giác ABNC nội tiếp \( \Rightarrow MB.MC = MA.MN\)
\( \Rightarrow MO.MD = MA.MN\) \( \Rightarrow \) Tứ giác AOND nội tiếp
\( \Rightarrow DO\) là phân giác \(\widehat {ADN}\)b) Xét \({\rm{\Delta }}DBP\) và \({\rm{\Delta }}DAB\) có
\(\widehat {BDP}\;\)chung; \(\widehat {DBP} = \widehat {DAB}\)
\( \Rightarrow {\rm{\Delta }}DBP \sim {\rm{\Delta }}DAB\) (g.g) \( \Rightarrow \frac{{AB}}{{BP}} = \frac{{AD}}{{DB}}\)
Tương tự ta có \({\rm{\Delta }}DCP \sim {\rm{\Delta }}DAC \Rightarrow \frac{{AC}}{{CP}} = \frac{{AD}}{{DC}}\)
\( \Rightarrow \frac{{AB}}{{BP}} = \frac{{AC}}{{CP}} \Rightarrow AB.CP = AC.BP\)
Áp dụng định lý Ptoleney cho tứ giác ABPC nội tiếp ta có
\(AP.BC = AB:CP + AC.BP\)
\( \Rightarrow 2AP.CM = 2AC.BP \Rightarrow \frac{{AP}}{{AC}} = \frac{{BP}}{{CM}}\)
\({\rm{\Delta }}ABP\) và \({\rm{\Delta }}AMC\) có \(\frac{{AP}}{{AC}} = \frac{{BP}}{{CM}}\;;\;\widehat {APB} = \widehat {ACM}\)
\( \Rightarrow {\rm{\Delta }}ABP \sim {\rm{\Delta }}AMC\) (c.g.c) \( \Rightarrow \widehat {ABP} = \widehat {AMC}\)
Lại có tứ giác ABPF nội tiếp nên \(\widehat {ABP} = {180^\diamondsuit } - \widehat {AFP}\)
Lại có tứ giác AMEF nội tiếp nên \(\widehat {AME} = {180^\diamondsuit } - \widehat {AFB}\)
\( \Rightarrow \widehat {AFP} = \widehat {AFE} \Rightarrow E,\;F,\;P\) thẳng hàngc) Áp dụng hệ thức lượng cho \({\rm{\Delta }}OCD\) vuông tại C ta có
\(OM.OD = O{C^2} = O{F^2} \Rightarrow \frac{{OF}}{{OM}} = \frac{{OD}}{{OF}}\) \( \Rightarrow {\rm{\Delta }}OMF \sim {\rm{\Delta }}OFD\;\) (c.g.c)
\( \Rightarrow \widehat {OFD} = \widehat {OMF} = {90^\diamondsuit } - \widehat {CMF} = {90^\diamondsuit } - \widehat {FAE} = {90^\diamondsuit } - \widehat {AFO}\;\)
\( \Rightarrow AFD = {90^\diamondsuit } \Rightarrow AF \bot FD\) mà \(AF \bot FK\)
\( \Rightarrow DF = DK \Rightarrow D,\;F,\;K\) thẳng hàng
Gọi \(Z,\;X\) là giao \(FN\) với \(BC,\;DM\).
Gọi \(T\) là giao \(KZ\) với \(MF\).
Ta có \(D{C^2} = DK.DF = DM.DO \Rightarrow \) Tứ giác OMKF nội tiếp
\( \Rightarrow \widehat {KMF} = \widehat {KOF\;} = 2\widehat {OAF} = 2\widehat {FMS}\;\)
\( \Rightarrow \widehat {KME} = \widehat {FME} = \widehat {FAO} = \widehat {KNF}\) \( \Rightarrow \) Tứ giác MNKZ nội tiếp
\( \Rightarrow \widehat {KZM} = {180^\diamondsuit } - \widehat {MNK} = {90^\diamondsuit }\)
Lại có \({\rm{\Delta }}TMK\) có MZ là đường cao đồng thời là phân giác
\( \Rightarrow ZT = ZK\)
Do \(TK//DM \Rightarrow \frac{{ZT}}{{MX}} = \frac{{FZ}}{{FX}} = \frac{{ZK}}{{DX}}\)
\( \Rightarrow XD = XM \Rightarrow \) X là trung điểm của đoạn DM.
Vậy FN đi qua trung điểm của đoạn DMĐăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1. Ta có:
\(P = \frac{{2a}}{{\sqrt {1 + {a^2}} }} + \frac{b}{{\sqrt {1 + {b^2}} }} + \frac{c}{{\sqrt {1 + {c^2}} }}\)
\( = \frac{{2a}}{{\sqrt {{a^2} + ab + bc + ca} }} + \frac{b}{{\sqrt {{a^2} + ab + bc + ca} }} + \frac{c}{{\sqrt {{a^2} + ab + bc + ca} }}\)
\( = \frac{{2a}}{{\sqrt {\left( {a + b} \right)\left( {a + c} \right)} }} + \frac{b}{{\sqrt {\left( {b + c} \right)\left( {b + a} \right)} }} + \frac{c}{{\sqrt {\left( {c + a} \right)\left( {c + b} \right)} }}\)
\( = \sqrt {\frac{{2a}}{{a + b}}.\frac{{2a}}{{a + c}}} + \sqrt {\frac{{2b}}{{b + a}}.\frac{b}{{2\left( {b + c} \right)}}} + \sqrt {\frac{{2c}}{{c + a}}.\frac{c}{{2\left( {c + b} \right)}}} \)
\(AM - GM\)
\( \le \frac{1}{2}\left[ {\frac{{2a}}{{a + b}} + \frac{{2a}}{{a + c}} + \frac{{2b}}{{b + a}} + \frac{b}{{2\left( {b + c} \right)}} + \frac{{2c}}{{c + a}} + \frac{c}{{2\left( {c + b} \right)}}} \right]\)
\( = \frac{1}{2}\left[ {\left( {\frac{{2a}}{{a + b}} + \frac{{2b}}{{a + b}}} \right) + \left( {\frac{{2a}}{{a + c}} + \frac{{2a}}{{a + c}}} \right) + \frac{1}{2}\left( {\frac{b}{{b + c}} + \frac{c}{{b + c}}} \right)} \right]\;\)
\( = \frac{1}{2}\left( {2 + 2 + \frac{1}{2}} \right) = \frac{9}{4}\)
Dấu “=” xảy ra khi \(a = \frac{{7\sqrt {15} }}{{15}};b = c = \frac{{\sqrt {15} }}{{15}}\)
Vậy P đạt GTLN là \(\frac{9}{4}\) khi \(a = \frac{{7\sqrt {15} }}{{15}};b = c = \frac{{\sqrt {15} }}{{15}}\)2. Ta có \(ab + bc + ca + abc \le 4\)
\( \Leftrightarrow abc + 2\left( {ab + bc + ca} \right) + 4\left( {a + b + c} \right) + 8 \le \left( {ab + 2a + 2b + 4} \right) + \left( {bc + 2b + 2c + 4} \right)\)
\( + \left( {ca + 2c + 2a + 4} \right)\)
\( \Leftrightarrow \left( {a + 2} \right)\left( {b + 2} \right)\left( {c + 2} \right) \le \left( {a + 2} \right)\left( {b + 2} \right) + \left( {b + 2} \right)\left( {c + 2} \right)\)
\( + \left( {c + 2} \right)\left( {a + 2} \right)\)
\( \Leftrightarrow 1 \le \frac{1}{{a + 2}} + \frac{1}{{b + 2}} + \frac{1}{{c + 2}} \Leftrightarrow \frac{2}{{a + 2}} + \frac{2}{{b + 2}} + \frac{2}{{c + 2}}\;\; \ge 2\)
\( \Leftrightarrow \left( {1 - \frac{2}{{a + 2}}} \right) + \left( {1 - \frac{2}{{b + 2}}} \right) + \left( {1 - \frac{2}{{c + 2}}} \right) \le 1\)
\( \Leftrightarrow 1 \ge \frac{a}{{a + 2}} + \frac{b}{{b + 2}} + \frac{c}{{c + 2}}\)
Áp dụng BĐT Cauchy-Schwarz
\(1 \ge \frac{a}{{a + 2}} + \frac{b}{{b + 2}} + \frac{c}{{c + 2}} = \frac{{{a^2}}}{{{a^2} + 2a}} + \frac{{{b^2}}}{{{b^2} + 2b}} + \frac{{{c^2}}}{{{c^2} + 2c}}\)
\(C - S \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{{{a^2} + {b^2} + {c^2} + 2\left( {a + b + c} \right)}}\)
\( \Rightarrow {\left( {a + b + c} \right)^2} \le \left( {{a^2} + {b^2} + {c^2}} \right) + 2\left( {a + b + c} \right)\)
\( \Leftrightarrow a + b + c \ge ab + bc + ca\) (đpcm)Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập