a) Ông A có một mảnh đất hình chữ nhật , chiều dài hơn chiều rộng \(15m\). Ông A quyết định bán đi một phần của mảnh đất đó. Mảnh đất cón lại sau khi bán vẫn là hình chữ nhật, nhưng so với lúc đầu thì chiều rộng đã giảm \(5m\), chiều dài không đổi và diện tích là \(300\)\({m^2}\). Tính chiều dài và chiều rộng của mảnh đất lúc đầu.
b) Giải phương trình \(\sqrt {{x^2} + 2x + 4} + \left( {x - 1} \right)\left( {x + 3} \right) + 1 = 0\)
a) Ông A có một mảnh đất hình chữ nhật , chiều dài hơn chiều rộng \(15m\). Ông A quyết định bán đi một phần của mảnh đất đó. Mảnh đất cón lại sau khi bán vẫn là hình chữ nhật, nhưng so với lúc đầu thì chiều rộng đã giảm \(5m\), chiều dài không đổi và diện tích là \(300\)\({m^2}\). Tính chiều dài và chiều rộng của mảnh đất lúc đầu.
b) Giải phương trình \(\sqrt {{x^2} + 2x + 4} + \left( {x - 1} \right)\left( {x + 3} \right) + 1 = 0\)
Quảng cáo
Trả lời:
a) Gọi \(x,y{\rm{ }}(m)\) là chiều dài và chiều rộng của mảnh đất lúc đầu (\(x,y > 0)\).
Ta có hệ phương trình \(\left\{ \begin{array}{l}x = y + 15\\\left( {y - 5} \right)x = 300\end{array} \right.\)
Ta có phương trình \(\left( {y - 5} \right)\left( {y + 15} \right) = 300 \Leftrightarrow {y^2} + 10y - 375 = 0 \Leftrightarrow \left[ \begin{array}{l}y = 15\\y = - 25\end{array} \right.\), chọn \(y = 15\) suy ra \(x = 30\).
Vậy chiều dài và chiều rộng lúc đầu của mảnh đất là \(20m\) và \(15m\).
b) Ta biến đổi \(\sqrt {{x^2} + 2x + 4} + \left( {x - 1} \right)\left( {x + 3} \right) + 1 = 0 \Leftrightarrow \sqrt {{x^2} + 2x + 4} + {x^2} + 2x + 4 - 6 = 0\)
Đặt \(t = \sqrt {{x^2} + 2x + 4} \), \(\left( {t > 0} \right)\) ta suy ra phương trình \({t^2} + t - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\\t = - 3\end{array} \right.\) chọn \(t = 2\)
Với \(t = 2\) ta có \(\sqrt {{x^2} + 2x + 4} = 2 \Leftrightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Vậy phương trình đã cho có hai nghiệm \(x = 0\) và \(x = 2\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
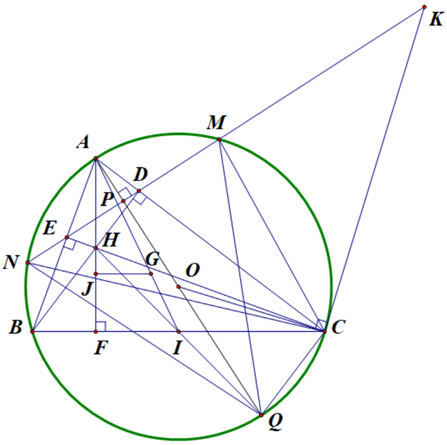
a) Xét tứ giác \(ADHE\) ta có \(\widehat D = \widehat E = 90^\circ \) suy ra \(\widehat D + \widehat E = 180^\circ \) do vậy tứ giác \(ADHE\) nội tiếp trong một đường tròn.
b) Ta có
Do \(CK\) là tiếp tuyến nên
Từ hai lập luận trên ta có . Vậy \(\widehat {KNC} = \widehat {KCM}\).
Xét hai tam giác \(\Delta KNC\) và \(\Delta KCM\) ta có \(\widehat {KNC} = \widehat {KCM}\) và góc \(K\) chung do đó \(\Delta KNC\) và \(\Delta KCM\) là hai tam giác đồng dạng, do vậy \(\frac{{KN}}{{KC}} = \frac{{KC}}{{KM}}\) hay \(K{C^2} = KM.KN\).
c) Theo hình vẽ ta có
\(\widehat {AED} = \widehat {AHD}\) (cùng chắn cung đường tròn \(\left( {O'} \right)\)
\( = \widehat {BHF}\) ( Hai góc đối đỉnh)
= \(\widehat {ACB}\) (cặp góc có cạnh tương ứng vuông góc).
Ta lại có \(\widehat {EAP} = \widehat {BAQ}\), mà \(\widehat {ACB} + \widehat {BAQ} = 90^\circ \) suy ra \(\widehat {AED} + \widehat {EAP} = 90^\circ \) từ đây suy ra \(\widehat {APE} = 90^\circ \) hay \(AQ \bot ED \Rightarrow AQ \bot MN\) do vậy \(AQ\) là đường trung trực của \(MN\) do vậy \(QM = QN\).
d) Ta có \(I\) là giao điểm của \(HQ\) và \(BC\)
Xét tứ giác \(HBQC\) ta có \(HB{\rm{//}}GC\) (vì cùng vuông góc với \(AC\))
Tương tự \(HC{\rm{//}}QB\) (vì cùng vuông góc với \(AB\))
Do đo tứ giác \(HBQC\) là hình bình hành, suy ra \(I\) là trung điểm của \(BC\).
Xét \(4\) điểm \(E,B,C,D\) cùng nằm trên đường tròn đường kính \(BC\), ta có hai tam giác \(\Delta EHD\) và \(\Delta BHC\) đồng dạng (g-g-g) theo tỷ số \(\frac{{ED}}{{BC}}\).
Hai \(\Delta BHC\) và \(\Delta ABC\) có đường cao lần lượt là \(HF\) và \(AF\) (cùng ứng với cạnh đáy \(BC\)) do đó \(\frac{{{S_{BHC}}}}{{{S_{ABC}}}} = \frac{{HF}}{{AF}}\).
Gọi \(G\) là trọng tâm của tam giác \(ABC\), qua \(G\) kẻ đường thẳng song song với \(BC\) cắt \[AF\] tại \[J\] ta có tỷ số \(\frac{{AJ}}{{AF}} = \frac{1}{3}\).
Ta có \(\frac{{{S_{HDE}}}}{{{S_{ABC}}}} = \frac{{{S_{HDE}}}}{{{S_{HBC}}}}.\frac{{{S_{HBC}}}}{{{S_{ABC}}}} = {\left( {\frac{{ED}}{{BC}}} \right)^2}.\frac{{HF}}{{AF}}\) (1)
Tiếp theo ta sẽ chứng minh \(\frac{{HF}}{{AF}} > \frac{1}{3}\) với giả thiết \(AB < AC < BC\) và \(\widehat A < 90^\circ \).
Vì \(\Delta ABF\) và \(\Delta CHF\) đồng dạng nên \(\frac{{AF}}{{BF}} = \frac{{CF}}{{HF}} \Rightarrow \frac{{FB}}{{FA}} = \frac{{FH}}{{FC}}\)
Trong tam giác \(ABC\) ta có \(\cot B.\cot C = \frac{{FB}}{{FA}}.\frac{{FC}}{{FA}} = \frac{{HF}}{{AF}}\) (2)
Mặt khác trong tam giác nhọn \(\Delta ABC\) thì ta có \(\cot A.\cot B + \cot B.\cot C + \cot C.\cot A = 1\) (vượt tầm lớp 9!)
Lại từ giả thiết \(AB < AC < BC\) suy ra \(C < B < A < 90^\circ \), từ đây ta lại có \(0 < \cot A < \cot B < \cot C\) do đó \(1 = \cot A.\cot B + \cot B.\cot C + \cot C.\cot A < \cot C.\cot B + \cot B.\cot C + \cot C.\cot B\)
hay \(\cot B.\cot C > \frac{1}{3}\) (3)
Từ \((1),(2),(3)\) ta có được \(\frac{{HF}}{{AF}} > \frac{1}{3}\) và \(\frac{{{S_{HDE}}}}{{{S_{ABC}}}} > \frac{1}{3}\frac{{E{D^2}}}{{B{C^2}}}\) (đpcm).
Lời giải
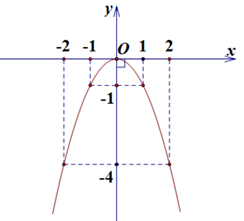
a) Ta có bảng giá trị sau
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
-4 |
-1 |
0 |
-1 |
-4 |
Do đó \((P)\) đi qua các điểm \(O\left( {0;0} \right),A\left( {1; - 1} \right),B\left( {2; - 4} \right),C\left( { - 1; - 1} \right)\) và \(D\left( { - 2; - 4} \right)\)
Parabol có bề lõm quay xuống dưới, nhận trục \(Oy\) làm trục đối xứng.
Vẽ
b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \({x^2} + 3x - m = 0\), biệt thức \(\Delta = 9 + 4m\).
Parabol và \(\left( d \right)\) cắt nhau tại hai điểm phân biệt khi và chỉ khi \(\Delta > 0 \Leftrightarrow m > - \frac{9}{4}\).
Lúc này các hoành độ giao điểm là \({x_1},{x_2}\) theo định lý Vi-et ta có \({x_1} + {x_2} = - 3;{x_1}{x_2} = - m\)
Yêu cầu bài toán \(5\left( {{x_1} + {x_2}} \right) = 1 - {\left( {{x_1}{x_2}} \right)^2} \Leftrightarrow - 15 = 1 - {\left( { - m} \right)^2} \Leftrightarrow {m^2} = 16 \Leftrightarrow m = \pm 4\)
Đối chiếu điều kiện chọn \(m = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.