Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Bà Rịa - Vũng Tàu có đáp án
40 người thi tuần này 4.6 83 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) Ta có \({x^2} - 5x + 4 = 0 \Leftrightarrow {x^2} - 4x + 4 - x = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\)
Vậy phương trình có hai nghiệm \(x = 1\) và \(x = 4\).
Cách 2: Ta có \(a + b + c = 0\) nên phương trình có một nghiệm \({x_1} = 1\) và nghiệm \({x_2} = \frac{c}{a} = 4\).
Vậy phương trình có hai nghiệm \(x = 1\) và \(x = 4\).
b) Ta có \(\left\{ \begin{array}{l}x + 2y = 3\\3x - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 4\\3x - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\3 - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\)
Vậy hệ có nghiệm \(\left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\).
c) Ta có \(P = \sqrt {20} - 3\sqrt {45} + \frac{{\sqrt {55} }}{{\sqrt {11} }} = 2\sqrt 5 - 3.3\sqrt 5 + \frac{{\sqrt 5 .\sqrt {11} }}{{\sqrt {11} }} = 2\sqrt 5 - 9\sqrt 5 + \sqrt 5 = - 6\sqrt 5 \)
Vậy \(P = - 6\sqrt 5 \)
Lời giải
a) Ta có bảng giá trị sau
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
-4 |
-1 |
0 |
-1 |
-4 |
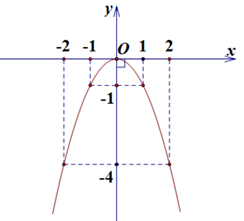
Do đó \((P)\) đi qua các điểm \(O\left( {0;0} \right),A\left( {1; - 1} \right),B\left( {2; - 4} \right),C\left( { - 1; - 1} \right)\) và \(D\left( { - 2; - 4} \right)\)
Parabol có bề lõm quay xuống dưới, nhận trục \(Oy\) làm trục đối xứng.
Vẽ
b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \({x^2} + 3x - m = 0\), biệt thức \(\Delta = 9 + 4m\).
Parabol và \(\left( d \right)\) cắt nhau tại hai điểm phân biệt khi và chỉ khi \(\Delta > 0 \Leftrightarrow m > - \frac{9}{4}\).
Lúc này các hoành độ giao điểm là \({x_1},{x_2}\) theo định lý Vi-et ta có \({x_1} + {x_2} = - 3;{x_1}{x_2} = - m\)
Yêu cầu bài toán \(5\left( {{x_1} + {x_2}} \right) = 1 - {\left( {{x_1}{x_2}} \right)^2} \Leftrightarrow - 15 = 1 - {\left( { - m} \right)^2} \Leftrightarrow {m^2} = 16 \Leftrightarrow m = \pm 4\)
Đối chiếu điều kiện chọn \(m = 4\).
Lời giải
a) Gọi \(x,y{\rm{ }}(m)\) là chiều dài và chiều rộng của mảnh đất lúc đầu (\(x,y > 0)\).
Ta có hệ phương trình \(\left\{ \begin{array}{l}x = y + 15\\\left( {y - 5} \right)x = 300\end{array} \right.\)
Ta có phương trình \(\left( {y - 5} \right)\left( {y + 15} \right) = 300 \Leftrightarrow {y^2} + 10y - 375 = 0 \Leftrightarrow \left[ \begin{array}{l}y = 15\\y = - 25\end{array} \right.\), chọn \(y = 15\) suy ra \(x = 30\).
Vậy chiều dài và chiều rộng lúc đầu của mảnh đất là \(20m\) và \(15m\).
b) Ta biến đổi \(\sqrt {{x^2} + 2x + 4} + \left( {x - 1} \right)\left( {x + 3} \right) + 1 = 0 \Leftrightarrow \sqrt {{x^2} + 2x + 4} + {x^2} + 2x + 4 - 6 = 0\)
Đặt \(t = \sqrt {{x^2} + 2x + 4} \), \(\left( {t > 0} \right)\) ta suy ra phương trình \({t^2} + t - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\\t = - 3\end{array} \right.\) chọn \(t = 2\)
Với \(t = 2\) ta có \(\sqrt {{x^2} + 2x + 4} = 2 \Leftrightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Vậy phương trình đã cho có hai nghiệm \(x = 0\) và \(x = 2\).
Lời giải
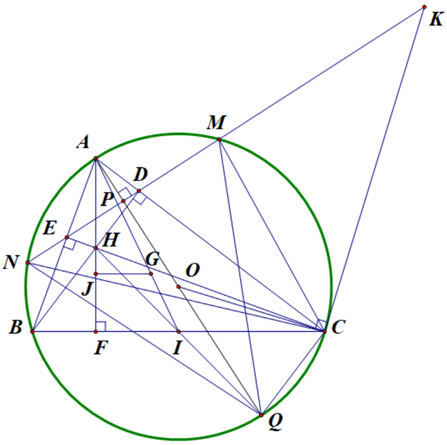
a) Xét tứ giác \(ADHE\) ta có \(\widehat D = \widehat E = 90^\circ \) suy ra \(\widehat D + \widehat E = 180^\circ \) do vậy tứ giác \(ADHE\) nội tiếp trong một đường tròn.
b) Ta có
Do \(CK\) là tiếp tuyến nên
Từ hai lập luận trên ta có . Vậy \(\widehat {KNC} = \widehat {KCM}\).
Xét hai tam giác \(\Delta KNC\) và \(\Delta KCM\) ta có \(\widehat {KNC} = \widehat {KCM}\) và góc \(K\) chung do đó \(\Delta KNC\) và \(\Delta KCM\) là hai tam giác đồng dạng, do vậy \(\frac{{KN}}{{KC}} = \frac{{KC}}{{KM}}\) hay \(K{C^2} = KM.KN\).
c) Theo hình vẽ ta có
\(\widehat {AED} = \widehat {AHD}\) (cùng chắn cung đường tròn \(\left( {O'} \right)\)
\( = \widehat {BHF}\) ( Hai góc đối đỉnh)
= \(\widehat {ACB}\) (cặp góc có cạnh tương ứng vuông góc).
Ta lại có \(\widehat {EAP} = \widehat {BAQ}\), mà \(\widehat {ACB} + \widehat {BAQ} = 90^\circ \) suy ra \(\widehat {AED} + \widehat {EAP} = 90^\circ \) từ đây suy ra \(\widehat {APE} = 90^\circ \) hay \(AQ \bot ED \Rightarrow AQ \bot MN\) do vậy \(AQ\) là đường trung trực của \(MN\) do vậy \(QM = QN\).
d) Ta có \(I\) là giao điểm của \(HQ\) và \(BC\)
Xét tứ giác \(HBQC\) ta có \(HB{\rm{//}}GC\) (vì cùng vuông góc với \(AC\))
Tương tự \(HC{\rm{//}}QB\) (vì cùng vuông góc với \(AB\))
Do đo tứ giác \(HBQC\) là hình bình hành, suy ra \(I\) là trung điểm của \(BC\).
Xét \(4\) điểm \(E,B,C,D\) cùng nằm trên đường tròn đường kính \(BC\), ta có hai tam giác \(\Delta EHD\) và \(\Delta BHC\) đồng dạng (g-g-g) theo tỷ số \(\frac{{ED}}{{BC}}\).
Hai \(\Delta BHC\) và \(\Delta ABC\) có đường cao lần lượt là \(HF\) và \(AF\) (cùng ứng với cạnh đáy \(BC\)) do đó \(\frac{{{S_{BHC}}}}{{{S_{ABC}}}} = \frac{{HF}}{{AF}}\).
Gọi \(G\) là trọng tâm của tam giác \(ABC\), qua \(G\) kẻ đường thẳng song song với \(BC\) cắt \[AF\] tại \[J\] ta có tỷ số \(\frac{{AJ}}{{AF}} = \frac{1}{3}\).
Ta có \(\frac{{{S_{HDE}}}}{{{S_{ABC}}}} = \frac{{{S_{HDE}}}}{{{S_{HBC}}}}.\frac{{{S_{HBC}}}}{{{S_{ABC}}}} = {\left( {\frac{{ED}}{{BC}}} \right)^2}.\frac{{HF}}{{AF}}\) (1)
Tiếp theo ta sẽ chứng minh \(\frac{{HF}}{{AF}} > \frac{1}{3}\) với giả thiết \(AB < AC < BC\) và \(\widehat A < 90^\circ \).
Vì \(\Delta ABF\) và \(\Delta CHF\) đồng dạng nên \(\frac{{AF}}{{BF}} = \frac{{CF}}{{HF}} \Rightarrow \frac{{FB}}{{FA}} = \frac{{FH}}{{FC}}\)
Trong tam giác \(ABC\) ta có \(\cot B.\cot C = \frac{{FB}}{{FA}}.\frac{{FC}}{{FA}} = \frac{{HF}}{{AF}}\) (2)
Mặt khác trong tam giác nhọn \(\Delta ABC\) thì ta có \(\cot A.\cot B + \cot B.\cot C + \cot C.\cot A = 1\) (vượt tầm lớp 9!)
Lại từ giả thiết \(AB < AC < BC\) suy ra \(C < B < A < 90^\circ \), từ đây ta lại có \(0 < \cot A < \cot B < \cot C\) do đó \(1 = \cot A.\cot B + \cot B.\cot C + \cot C.\cot A < \cot C.\cot B + \cot B.\cot C + \cot C.\cot B\)
hay \(\cot B.\cot C > \frac{1}{3}\) (3)
Từ \((1),(2),(3)\) ta có được \(\frac{{HF}}{{AF}} > \frac{1}{3}\) và \(\frac{{{S_{HDE}}}}{{{S_{ABC}}}} > \frac{1}{3}\frac{{E{D^2}}}{{B{C^2}}}\) (đpcm).
Lời giải
Ta có \(a + {b^3} = 29 \Leftrightarrow a = 29 - {b^3}\) do đó \(P = {a^2} + {b^4} - 19 = {\left( {29 - {b^3}} \right)^2} + {b^4} - 19 = {b^6} + {b^4} - 58{b^3} + 822\)
Ta có \(P = {b^6} + {b^4} - 58{b^3} + 822 = {b^6} + {b^4} - 58{b^3} + 756 + 66\) \( = {\left( {b - 3} \right)^2}.\left( {{b^4} + 6{b^3} + 28{b^2} + 56b + 84} \right) + 66\)
Do \({b^4} + 6{b^3} + 28{b^2} + 56b + 84 > 0,\forall b > 0\) nên \(P = {\left( {b - 3} \right)^2}.\left( {{b^4} + 6{b^3} + 28{b^2} + 56b + 84} \right) + 66 \ge 66\)
Dấu bằng xảy ra khi \(b = 3\).
Vậy \(\min P = 66\) khi \(\left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\).
Cách 2: Áp dụng bất đẳng thức Cô si cho \(n\) số dương tổng quát ta có \({a^2} + 4 \ge 4a\) và
\({b^4} + {b^4} + {b^4} + {3^4} \ge 4.\sqrt[4]{{{{\left( {{b^4}} \right)}^3}{{.3}^4}}} = 12{b^3}\) suy ra \(3{b^4} + 81 \ge 12{b^3}\) hay \({b^4} + 27 \ge 4{b^3}\)
Do đó \({a^2} + {b^4} + 31 \ge 4a + 4{b^3} = 116\) hay \(P = {a^2} + {b^4} - 19 \ge 66\)
Dấu bằng xảy ra ở các BĐT trên là \(a = 2\) và \(b = 3\).
Vậy \(\min P = 66\) khi \(\left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\).