Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Nghệ An có đáp án

a) \(\begin{array}{l}A = \sqrt 4  + \sqrt {49}  + \sqrt {64} \\A = 2 + 7 + 8\\A = 17\end{array}\)

b)          \(P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) \cdot \frac{{4x}}{{x - 1}}\) (x > 0 và \(x \ne 1\))

\(\begin{array}{l}P = \left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) \cdot \frac{{4x}}{{x - 1}}\\P = \left( {\frac{{x - 1}}{{2\sqrt x }}} \right) \cdot \frac{{4x}}{{x - 1}}\\P = 2\sqrt x \end{array}\)

c)          Vì đường thẳng y = 2x + b – 1 cắt trục hoành tại điểm có hoành độ bằng 1

Nên thay x = 1; y = 0 vào y = 2x + b – 1 ta được \[{\rm{ }}b{\rm{  +  }}1 = 0 \Leftrightarrow b =  - 1\]

Vậy b = -1

a) Giải phương trình \({x^2} + 3x - 10 = 0\)

\(\begin{array}{l}\Delta  = {b^2} - 4ac\\\Delta  = {3^2} - 4 \cdot 1 \cdot \left( { - 10} \right) = 49 > 0\end{array}\)

Nên phương trình có hai nghiệm phân biệt \({x_1} = \frac{{ - b - \sqrt \Delta  }}{{2a}} = \frac{{ - 3 - \sqrt {49} }}{2} =  - 5\); \({x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}} = \frac{{ - 3 + \sqrt {49} }}{2} = 2\)

Vậy tập nghiệm của phương trình là \(S = \left\{ { - 5;2} \right\}\)

b)    Phương trình \({x^2} - 5x + 3 = 0\) có \(\Delta  = {\left( { - 5} \right)^2} - 4 \cdot 3 = 13 > 0\)nên phương trình có hai nghiệm phân biệt x1, x2.

Theo định lý Viets ta có \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 5}\\{{x_1} \cdot {x_2} = 3}\end{array}} \right.\)

Vì \({x_1} + {x_2} = 5 > 0;\,\,\,{x_1} \cdot {x_2} = 3 > 0\) nên phương trình có hai nghiệm dương và do x1 là nghiệm của phương trình (1) nên \({x_1}^2 - 5{x_1} + 3 = 0\, \Rightarrow {x_1}^2 = 5{x_1} - 3\)

Do đó

\(\begin{array}{l}T = \frac{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{{x_1}^2 + 5{x_2}}}\\T = \frac{{{x_1} \cdot {x_2} + {x_1} + {x_2} + 1}}{{5\left( {{x_1} + {x_2}} \right) - 3}} = \frac{{3 + 5 + 1}}{{5 \cdot 5 - 3}} = \frac{9}{{22}}\end{array}\)

a)Gọi x (xe) là số xe loại I của một cửa hàng (x > 0)

Số xe loại II của một của hàng là 50 – x (xe)

Số tiền phải thanh toán xe loại I là 2x (triệu đồng)

Số tiền phải thanh toán xe loại II là 6(50-x) (triệu đồng)

Tổng số tiền cửa hàng phải thanh toán là 160 triệu đồng nên ta có phương trình :

\[\begin{array}{l}{\bf{2x}}{\rm{ }} + {\rm{ }}{\bf{6}}\left( {{\bf{50}}{\rm{ }}--{\rm{ }}{\bf{x}}{\rm{ }}} \right){\rm{ }} = {\rm{ }}{\bf{160}}\\ \Leftrightarrow  - 4x =  - 140\\ \Leftrightarrow x = 35(n)\end{array}\]

Vậy xe loại I là 35 xe

Xe loại II là 15 xe

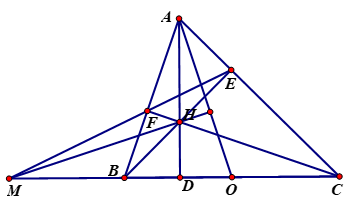
a)  Tứ giác AEHF có:

\(\begin{array}{l}\widehat {{\rm{AEH}}} = {90^0}\left( {BE \bot AC} \right)\\\widehat {{\rm{AFH}}} = {90^0}\left( {CF \bot AB} \right)\end{array}\)

\( \Rightarrow \widehat {{\rm{AEH}}} + \widehat {{\rm{AFH}}} = {180^0}\)

Suy ra tứ giác AEHF nội tiếp ( tổng hai góc đối bằng 1800)

b)    Chứng minh \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OFC}}}\)

Ta có \(\widehat {{\rm{BAD}}} = \widehat {{\rm{FCB}}}\) (cùng phụ với \(\widehat {{\rm{ACB}}}\)) hay \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OCF}}}\) (1)

Mặt khác \(\Delta BFC\) vuông tại F có FO là đường trung tuyến nên FO = OC

Suy ra \(\Delta FCO\)cân tại O suy ra \(\widehat {{\rm{OCF}}} = \widehat {{\rm{OFC}}}\)(2)

Từ (1) và (2) suy ra \(\widehat {{\rm{FAD}}} = \widehat {{\rm{OFC}}}\)

Chứng minh \(O{C^2} = OD \cdot OM\)

Ta dễ dàng chứng minh được các tứ giác AFDC; BFEC nội tiếp

Suy ra \(\widehat {{\rm{BDF}}} = \widehat {{\rm{BAC}}}\)(góc ngoài bằng góc trong tại đỉnh đối)

Lại có \(\widehat {{\rm{ODF}}} = {180^0} - \widehat {{\rm{BDF}}} = {180^0} - \widehat {{\rm{BAC}}}\) (3)

Mặt khác \(\widehat {{\rm{OFM}}} = \widehat {{\rm{OFB}}} + \widehat {{\rm{BFM}}} = \widehat {{\rm{OFB}}} + \widehat {{\rm{AFE}}}\)(\(\widehat {{\rm{BFM}}};\widehat {{\rm{AFE}}}\)đối đỉnh)

Mà \(\left\{ {\begin{array}{*{20}{c}}{\widehat {{\rm{AFE}}} = \widehat {{\rm{ACB}}}}\\{\widehat {{\rm{ACB}}} = \widehat {{\rm{OFB}}}}\end{array}} \right.\)   Suy ra \(\widehat {{\rm{OFM}}} = \widehat {{\rm{ABC}}} + \widehat {{\rm{ACB}}} = {180^0} - \widehat {{\rm{BAC}}}\)(4)

Từ (3) và (4) suy ra \(\widehat {{\rm{ODF}}} = \widehat {{\rm{OFM}}}\)

Xét \(\Delta OFD\)và \(\Delta OMF\)có:\(\widehat {{\rm{ODF}}} = \widehat {{\rm{OFM}}}\)(cmt);  \(\widehat {MOF}\)chung

Suy ra \(\Delta OFD\)\( \sim \Delta OMF\)(gg)

Suy ra \[\frac{{FO}}{{OM}} = \frac{{OD}}{{FO}}{\rm{O}}{{\rm{F}}^2} = OM \cdot OD = O{C^2}\](vì O là trung điểm BC)

c)

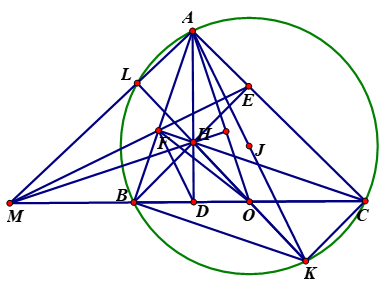
Gọi AK là đường kính của đường tròn ngoại tiếp tam giác ABC

Suy ra AB vuông góc với BK mà CH vuông góc với AB nên CH song song với BK

Chứng minh tương tự BH song song với CK

Do đó tứ giác BHCK là hình bình hành nên ba điểm O. H, K thẳng hàng (1).

Gọi L là giao điểm của AM với đường tròn ngoại tiếp tam giác ABC

Do các tứ giác ALBC và BFEC nội tiếp nên ta có

ML.MA=MB.MC=MF.ME

Suy ra tứ giac ALFE nội tiếp nên suy ra \(\widehat {{\rm{ALH}}} = \widehat {{\rm{AFH}}} = {90^0}\) (cùng chắn cung AH)

Suy ra AL vuông góc với HL.

Mà AL vuông góc với LK (góc nội tiếp chắn nữa đường tròn)

Nên bốn điểm L, H, O, K thảng hàng do đó OL vuông góc với AM

Vậy H là trực tâm của tam giác AMO  suy ra MH vuông góc với AO