Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Sóc Trăng năm học 2025-2026 có đáp án

        Ta có \(A = \sqrt {100}  + 3\sqrt 8  - 2\sqrt {18} \)

\(A = 10 + 3\sqrt {4.2}  - 2\sqrt {9.2} \)

\(A = 10 + 3.2\sqrt 2  - 2.3\sqrt 2 \)

\(A = 10 + 6\sqrt 2  - 6\sqrt 2 \)

\(A = 10\)

b) \(\left\{ \begin{array}{l}3x + y = 1\\x + y = 1\end{array} \right.\)

  \(\left\{ \begin{array}{l}2x = 0\\x + y = 1\end{array} \right.\)

\(\left\{ \begin{array}{l}x = 0\\0 + y = 1\end{array} \right.\)

 \(\left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {0;1} \right)\)

c)   \(5x \ge x - 6\)

\(5x - x \ge  - 6\)

\(4x \ge  - 6\)

  \(x \ge \frac{{ - 3}}{2}\)

Vậy nghiệm của bất phương trình là \(x \ge \frac{{ - 3}}{2}\)

a)

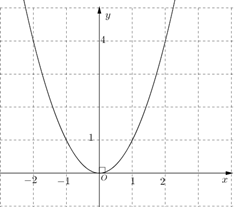
b)     Gọi điểm \(A\) có tọa độ \(\left( {m;n} \right)\)

Vì điểm \(A\) có hoành độ bằng \(5\) nên \(m = 5\)

Vì điểm \(A\) nằm trên đường thẳng \(d:y = 3x + 1\) nên ta có

        \(\begin{array}{l}n = 3m + 1\\n = 3.5 + 1\\n = 16\end{array}\)

Khi đó điểm \(A\) có tọa độ là \(\left( {5;16} \right)\)

Vì tọa độ các điểm nằm trên đồ thị \(\left( P \right)\)  có cùng tung độ với điểm \(A\) nên thay \(y = 16\) vào \(y = {x^2}\) , ta được

        \({x^2} = 16\)

      \(x = 4\)  hoặc \(x =  - 4\)

Vậy tọa độ các điểm nằm trên đồ thị \(\left( P \right)\) có cùng tung độ với điểm \(A\)  là \(\left( {4;16} \right)\) và \(\left( { - 4;16} \right)\)

a)    Gọi vận tốc của ông An là \(x\left( {km/h,x > 0} \right)\)

     Vận tốc của ông Bình là \(x + 10\left( {km/h} \right)\)

      Thời gian ông An đi từ nhà đến cơ quan là \(\frac{{50}}{x}\) (giờ)

      Thời gian ông Bình đi từ nhà đến cơ quan là \(\frac{{60}}{{x + 10}}\) (giờ)

       Vì hai người đến cơ quan cùng lúc nên ta có phương trình

                      \(\frac{{50}}{x} = \frac{{60}}{{x + 10}}\)

                  \(50x + 500 = 60x\)

                             \(10x = 500\)

                                 \(x = 50\) (TMĐK)

          Thời gian ông An đi từ nhà đến cơ quan là \(\frac{{50}}{{50}} = 1\) (giờ)

           Vậy ông An và ông Bình đến cơ quan lúc \(7\) giờ.

b) Vì mỗi vòng xoay có thể cài đặt một chữ số từ \(0\) đến \(9\) nên mỗi vòng xoay có \(10\)cách cài đặt. Do đó số kết quả có thể xảy ra là \(10.10.10 = 1000\)

Có 10 kết quả thuận lợi cho biến cố \(A\) là: \(\left( {0;0;0} \right)\); \(\left( {1;1;1} \right)\); \(\left( {2;2;2} \right)\); \(\left( {3;3;3} \right)\); \(\left( {4;4;4} \right)\); \(\left( {5;5;5} \right)\); \(\left( {6;6;6} \right)\); \(\left( {7;7;7} \right)\); \(\left( {8;8;8} \right)\); \(\left( {9;9;9} \right)\).

Xác suất của biến cố \(A\) là \(\frac{{10}}{{1000}} = \frac{1}{{100}}\)

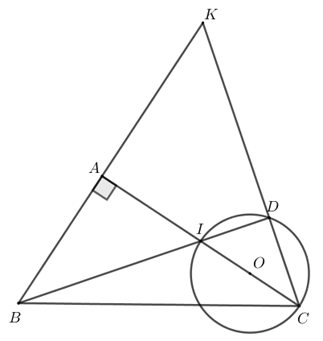
a)   Do \(D\) thuộc đường tròn đường kính \(IC\) nên \(\widehat {IDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

      Khi đó \(\Delta BDC\) vuông tại \(D\) nên \(B,D,C\) cùng thuộc đường tròn đường kính \(BC\)

      Tương tự \(\Delta ABC\) vuông tại \(A\) nên \(B,A,C\) cùng thuộc đường tròn đường kính \(BC\)

Vậy tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(BC\)

b)  Xét \(\Delta IDC\) và \(\Delta IAB\) có

      \(\widehat {DIC} = \widehat {AIB}\) (hai góc đối đỉnh)

      \(\widehat {CDI} = \widehat {IAB} = 90^\circ \)

      Do đó \(\Delta IDC\)\(\Delta IAB\) (g.g)

      Nên \(\frac{{ID}}{{IA}} = \frac{{IC}}{{IB}}\) hay \(IA.IC = IB.ID\)

   c) Vì \(I\) là trung điểm của \(AC\) nên \(IC = \frac{1}{2}AC = 2\) (cm)

                                                Mà \(\Delta ABC\) vuông tại \(A\) nên \(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\) suy ra \(BC = 5\) (cm)

                            Gọi \(E\) là giao điểm thứ hai của \(BC\) với đường tròn tâm \(O\)

                            Xét \(\Delta KBC\) có \(BD,CA\) là đường cao cắt nhau tại \(I\) nên \(I\) là trực tâm của \(\Delta KBC\)

                            Khi đó \(KI \bot BC\)

                            Lại có \(E\) thuộc đường tròn tâm \(O\) nên \(\widehat {IEC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

                            Hay \(IE \bot BC\)

                            Vậy \(K,I,E\) thẳng hàng

                            Xét \(\Delta CIE\) và \(\Delta CBA\) có

                            \(\widehat {ACB}\)  góc chung

                            \(\widehat {CEI} = \widehat {CAB} = 90^\circ \)

                            Nên \(\Delta CBA\) (g.g)

                            Suy ra \(\frac{{CI}}{{CB}} = \frac{{IE}}{{AB}}\) hay \(IE = \frac{{CI.AB}}{{CB}} = \frac{{2.3}}{5} = \frac{6}{5}\) (cm)

                            Khi đó \(C{E^2} = C{I^2} - I{E^2} = {2^2} - {\left( {\frac{6}{5}} \right)^2} = \frac{{64}}{{25}}\) hay \(CE = \frac{8}{5}\) (cm)

                            Suy ra \(BE = BC - CE = 5 - \frac{8}{5} - \frac{{17}}{5}\) (cm)

                            Ta có \(\tan \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{4}{3}\)

                            Mà \(\tan \widehat {KBE} = \frac{{KE}}{{BE}} = \tan \widehat {ABC} = \frac{4}{3}\) nên \(KE = \frac{4}{3}.BE = \frac{4}{3}.\frac{{17}}{5} = \frac{{68}}{{15}}\) (cm)

                            Vậy \(IK = KE - IE = \frac{{68}}{{15}} - \frac{6}{5} = \frac{{10}}{3}\) (cm)