Đề minh họa thi vào lớp 10 môn Toán năm 2026 TP. Hồ Chí Minh
287 người thi tuần này 4.6 1.2 K lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) Ta có bảng giá trị sau:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = - \frac{1}{2}{x^2}\) |
\( - 2\) |
\( - 0,5\) |
0 |
\( - 0,5\) |
\( - 2\) |
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0\,;\,\,0} \right);\,\,A\left( { - 2\,;\,\, - 2} \right);\,\,B\left( { - 1\,;\,\, - 0,5} \right);\,\,\)\(C\left( {1\,;\,\, - 0,5} \right);\,\,\)\(D\left( {2\,;\,\, - 2} \right).\)
Hệ số \(a = \frac{1}{2} < 0\) nên parabol có bề lõm hướng xuống. Đồ thị hàm số nhận \(Oy\) làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(\left( P \right):y = - \frac{1}{2}{x^2}\) như sau:
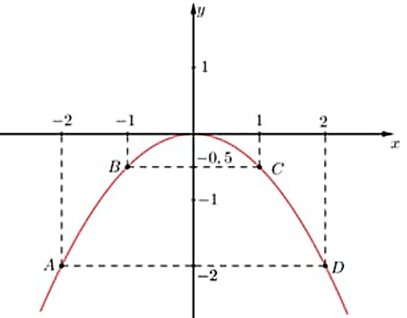
b) Gọi \(M\left( {{x_M};\,\,{y_M}} \right)\) là một điểm thuộc \(\left( P \right).\)
Vì \(M\) có hoành độ bằng tung độ nên:
\({x_M} = - \frac{1}{2}x_M^2\)
\(2{x_M} + x_M^2 = 0\)
\({x_M}\left( {2 + {x_M}} \right) = 0\)
Có hai giá trị thỏa mãn là \({x_M} = 0\) (loại vì điểm cần tìm khác gốc tọa độ); \({x_M} = - 2.\)
Vậy điểm thuộc \(\left( P \right)\) có hoành độ bằng tung độ là \(\left( { - 2\,;\,\, - 2} \right).\)
Lời giải
a) Phương trình \({x^2} - 5x + 1 = 0\) có \(a = 1\,;\,\,b = - 5\,;\,\,c = 1.\)
Ta có \(\Delta = {b^2} - 4ac = {\left( { - 5} \right)^2} - 4 \cdot 1 \cdot 1 = 21 > 0.\)
Vậy phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
b) Ta có \(A = {\left( {{x_1} - {x_2}} \right)^2} - 2{x_1} - 2{x_2}\)
\( = x_{_1}^2 - 2{x_1}{x_2} + x_{_2}^2 - 2\left( {{x_1} + {x_2}} \right)\)
\( = \left( {x_{_1}^2 + 2{x_1}{x_2} + x_{_2}^2 - 4{x_1}{x_2}} \right) - 2\left( {{x_1} + {x_2}} \right)\)
\[ = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right).\]
Theo định lí Viète, ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 5\\{x_1}{x_2} = \frac{c}{a} = 1\end{array} \right.,\) thay vào biểu thức \(A,\) ta được: \(A = {5^2} - 4 \cdot 1 - 2 \cdot 5 = 11.\)
Vậy \(A = 11.\)
Lời giải
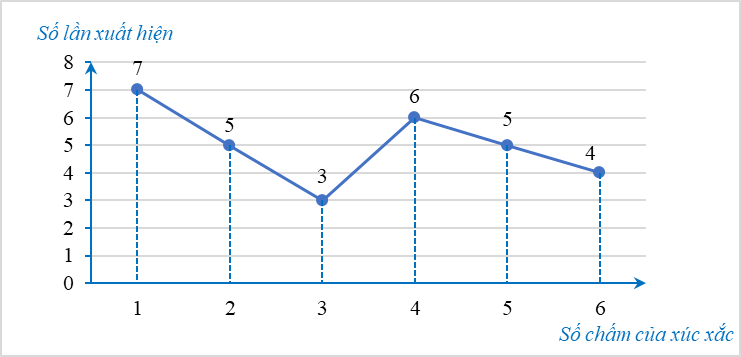
a) Tổng số lần gieo xúc xắc là: \(7 + 5 + 3 + 6 + 5 + 4 = 30\) (lần).
Tổng số chấm sau các lần gieo là: \(7 \cdot 1 + 5 \cdot 2 + 3 \cdot 3 + 6 \cdot 4 + 5 \cdot 5 + 4 \cdot 6 = 99\) (chấm).
Giá trị trung bình cộng về số chấm sau các lần gieo của bạn A là: \(\frac{{99}}{{30}} \approx 3\) (chấm).
Vậy giá trị trung bình cộng về số chấm sau các lần gieo của bạn A là 3 chấm.
b) Số lần xuất hiện mặt 2 chấm là 5 lần.
Xác suất thực nghiệm của biến cố A: “Số chấm xuất hiện trên mặt con xúc xắc là số 2” là: \(\frac{5}{{30}} = \frac{1}{6}.\)
c) Số lần xuất hiện mặt số chấm lớn hơn 3 (tức là 4 chấm, 5 chấm, 6 chấm) là: \(6 + 5 + 4 = 15\) (chấm).
Xác suất thực nghiệm của biến cố B: “Số chấm xuất hiện trên mặt con xúc xắc là một số lớn hơn 3” là:
\(\frac{{15}}{{30}} = \frac{1}{2}.\)
Câu 4
|
(1,0 điểm) Một khu vườn hình chữ nhật có chiều rộng là \(x\) (mét), chiều dài là \(y\) (mét). Bác Cường dự định xây một cái hồ hình tròn tiếp xúc với các cạnh của khu vườn như hình vẽ.
|
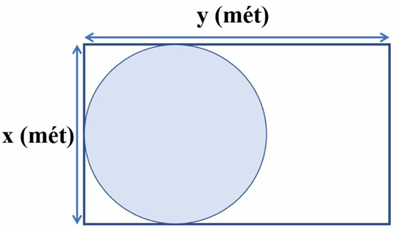 |
b) Biết rằng khu vườn hình chữ nhật có chiều dài gấp hai lần chiều rộng và diện tích phần còn lại của khu vườn \(77,76\,\,{{\rm{m}}^{\rm{2}}}.\) Tìm các kích thước ban đầu của khu vườn. (Lấy giá trị
Lời giải
a) Diện tích khu vườn hình chữ nhật là: \(xy\,\,\left( {{{\rm{m}}^2}} \right).\)
Bán kính hồ hình tròn tiếp xúc với các cạnh của khu vườn là: \[\frac{x}{2}\,\,({\rm{m}}).\]
Diện tích hồ hình tròn là: \[\pi \cdot {\left( {\frac{x}{2}} \right)^2} = \frac{{\pi {x^2}}}{4}\,\,\left( {{{\rm{m}}^2}} \right).\]
Vậy diện tích phần còn lại của khu vườn sau khi xây hồ là \[\frac{{\pi {x^2}}}{4}\,\,\left( {{{\rm{m}}^2}} \right).\]
b) Vì khu vườn hình chữ nhật có chiều dài gấp hai lần chiều rộng nên \(y = 2x.\)
Diện tích phần còn lại của khu vườn là \(77,76\,\,{{\rm{m}}^{\rm{2}}}\) nên ta có
\(xy - \frac{{\pi {x^2}}}{4} = 77,76\)
\(x \cdot 2x - \frac{{\pi {x^2}}}{4} = 77,76\)
\(8{x^2} - \pi {x^2} = 311,04\)
\({x^2}\left( {8 - \pi } \right) = 311,04\)
\({x^2}\left( {8 - \pi } \right) = 311,04\)
\({x^2} \approx 64\)
\(x = - 8\) (loại) hoặc \(x = 8\) (thỏa mãn).
Câu 5
|
(1,0 điểm) Bác Nam có một khối gỗ có dạng hình trụ với chiều cao là \(40\,\,{\rm{cm}}\) và đường kính đáy là \(20\,\,{\rm{cm}}{\rm{.}}\) Bác Nam muốn tiện khối gỗ này thành một vật trang trí có dạng hình nón có cùng chiều cao và bán kính với khối hình trụ ban đầu. |
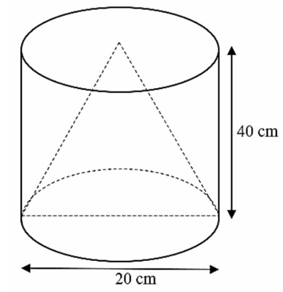 |
a) Tính thể tích phần gỗ bỏ đi khi thực hiện việc tiện gỗ hình trụ thành vật trang trí hình nón.
b) Sau khi hoàn thành sản phẩm, bác Nam dự tính phun sơn bề mặt bên ngoài của vật trang trí. Tính diện tích cần phải phun sơn (bao gồm cả mặt đáy).
(Các kết quả làm tròn chính xác đến hàng phần trăm của đơn vị)
Biết công thức tính thể tích khối trụ là \(V = \pi {R^2}h\) \((R\) là bán kính đáy, \(h\) là chiều cao); công thức tính thể tích hình nón là \(V = \frac{1}{3}\pi {R^2}h;\) công thức tính diện tích xung quanh hình nón là \(S = \pi Rl\) (\(l\) là độ dài đường sinh).
Lời giải
a) Thể tích khối gỗ dạng hình trụ là:
\({V_T} = \pi {R^2}h = \pi \cdot {10^2} \cdot 40 = 4000\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
Thể tích khối gỗ dạng hình nón là:
\({V_N} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi \cdot {10^2} \cdot 40 = \frac{{4000\pi }}{3}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
Thể tích phần khối gỗ bỏ đi khi thực hiện việc tiện gỗ hình trụ thành vật trang trí hình nón là:
\(V = {V_T} - {V_N} = 4000\pi - \frac{{4000\pi }}{3} \approx 8377,58\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
Vậy thể tích phần gỗ bỏ đi khi thực hiện việc tiện gỗ hình trụ thành vật trang trí hình nón khoảng \(8377,58\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\)
b) Đường sinh của hình nón là:
\(l = \sqrt {{h^2} + {R^2}} = \sqrt {{{40}^2} + {{10}^2}} = \sqrt {1700} \,\,\left( {{\rm{cm}}} \right).\)
Diện tích xung quanh hình nón là:
\({S_{xq}} = \pi Rl = \pi \cdot 10 \cdot \sqrt {1700} = 100\sqrt {17} \pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Diện tích mặt đáy là:
Diện tích cần phủ sơn là:
Vậy diện tích cần phủ sơn khoảng \(1609,47\,\,{\rm{c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.