(3,0 điểm) Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(O.\) Vẽ đường kính \(A\) của đường tròn \(\left( O \right)\) và đường cao \(AH\) của tam giác \(ABC.\)
a) Chứng minh \(\widehat {ACD} = 90^\circ \) và \(AB \cdot AC = AH \cdot AD.\)
b) Vẽ \[CF \bot AD,\] chứng minh rằng \(A{C^2} = AF \cdot AD\) và \(\widehat {CHF} = \widehat {DCF}.\)
c) Vẽ \[BK \bot AC,\,\,BK\] cắt \(AH\) tại \(I.\) Giả sử \(\widehat {BAC} = 60^\circ ,\,\,BC = 10\,\,{\rm{cm}},\) tính độ dài \(AI.\)
(3,0 điểm) Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(O.\) Vẽ đường kính \(A\) của đường tròn \(\left( O \right)\) và đường cao \(AH\) của tam giác \(ABC.\)
a) Chứng minh \(\widehat {ACD} = 90^\circ \) và \(AB \cdot AC = AH \cdot AD.\)
b) Vẽ \[CF \bot AD,\] chứng minh rằng \(A{C^2} = AF \cdot AD\) và \(\widehat {CHF} = \widehat {DCF}.\)
c) Vẽ \[BK \bot AC,\,\,BK\] cắt \(AH\) tại \(I.\) Giả sử \(\widehat {BAC} = 60^\circ ,\,\,BC = 10\,\,{\rm{cm}},\) tính độ dài \(AI.\)
Quảng cáo
Trả lời:

a) Vì \(\widehat {ACD}\) chắn nửa đường tròn \(\left( O \right)\) nên \(\widehat {ACD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta ABH\) và \(\Delta ADC\) có
\(\widehat {AHB} = \widehat {ACD} = 90^\circ ;\)
\(\widehat {ABH} = \widehat {ADC}\) (góc nội tiếp cùng chắn cung \(AC).\)
Do đó
Suy ra \(\frac{{AB}}{{AD}} = \frac{{AH}}{{AC}}\) hay \(AB \cdot AC = AH \cdot AD\) (đpcm).
b) Xét \(\Delta AFC\) và \(\Delta ACD\) có:
\(\widehat {CAD}\) chung; \(\widehat {AFC} = \widehat {ACD} = 90^\circ .\)
Do đó
Suy ra \(\frac{{AF}}{{AC}} = \frac{{AC}}{{AD}}\) hay \(AF \cdot AD = A{C^2}\) (đpcm).
Ta có \(\Delta AFC\) vuông tại \(F\) nên \(A,\,\,F,\,\,C\) cùng thuộc đường tròn đường kính \(AC\,;\)
\(\Delta AHC\) vuông tại \(H\) nên \(A,\,\,H,\,\,C\) cùng thuộc đường tròn đường kính \(AC\,.\)
Do đó \(A,\,\,F,\,\,C,\,\,H\) cùng thuộc đường tròn đường kính \(AC\,.\)
Suy ra \(\widehat {CHF} = \widehat {CAF}\) (góc nội tiếp cùng chắn cung \(CF).\) (1)
Ta có \(\widehat {CAF} + \widehat {ACF} = 90^\circ \) (do \(\Delta AFC\) vuông tại \(F)\) và \(\widehat {FCD} + \widehat {ACF} = 90^\circ .\) Suy ra \(\widehat {CAF} = \widehat {FCD}.\) (2)
Từ (1) và (2) suy ra \(\widehat {CHF} = \widehat {DCF}\) (đpcm).
c) Vì \(\Delta ABC\) có \(BK,\,\,AH\) là đường cao cắt nhau tại \(I\) nên \(I\) là trực tâm của \(\Delta ABC.\) Khi đó \(CI \bot AB.\)
Mà \(BD \bot AB\) (do \(\widehat {ABD}\) nội tiếp chắn nửa đường tròn) nên \(CI\,{\rm{//}}\,BD.\)
Lại có \(BI\,{\rm{//}}\,CD\) (do cùng vuông góc với \(AC)\)
Do đó \(BICD\) là hình bình hành.
Gọi \(M\) là giao điểm của \(DI\) và \(BC.\)
Khi đó \(M\) là trung điểm của \(DI\) và \(BC\) (tính chất hình bình hành).
Xét \(\Delta DAI\) có \(O\) là trung điểm của \(AD\) và \(M\) là trung điểm của \(DI\) nên \(OM\) là đường trung bình của \(\Delta DAI.\)
Suy ra \(OM = \frac{1}{2}AI\) hay \(AI = 2OM.\)
Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ = 120^\circ \) (góc nội tiếp chắn cung \(BC).\)
Vì \(\Delta BOC\) cân tại \(O\) có \(OM\) là đường trung tuyến nên \(OM\) đồng thời là phân giác của \(\widehat {BOC}\) và cũng là đường cao của \(\Delta BOC.\)
Khi đó \(\widehat {BOM} = \frac{1}{2}\widehat {BOC} = 60^\circ .\)
Xét \(\Delta BOM\) vuông tại \(M\) có: \[OM = BM \cdot \cot \widehat {MOB} = \frac{1}{2}BC \cdot \cot \widehat {MOB} = \frac{1}{2} \cdot 10 \cdot \cot 60^\circ = \frac{{5\sqrt 3 }}{3}\,\,\left( {{\rm{cm}}} \right).\]
Vậy \[AI = 2 \cdot OM = \frac{{10\sqrt 3 }}{3}\,\,\left( {{\rm{cm}}} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
|
(1,0 điểm) Một khu vườn hình chữ nhật có chiều rộng là \(x\) (mét), chiều dài là \(y\) (mét). Bác Cường dự định xây một cái hồ hình tròn tiếp xúc với các cạnh của khu vườn như hình vẽ.
|
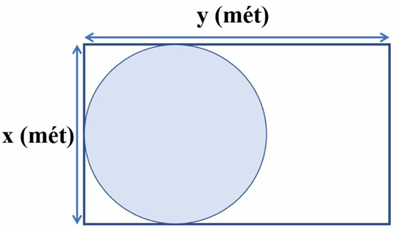 |
b) Biết rằng khu vườn hình chữ nhật có chiều dài gấp hai lần chiều rộng và diện tích phần còn lại của khu vườn \(77,76\,\,{{\rm{m}}^{\rm{2}}}.\) Tìm các kích thước ban đầu của khu vườn. (Lấy giá trị
Lời giải
a) Diện tích khu vườn hình chữ nhật là: \(xy\,\,\left( {{{\rm{m}}^2}} \right).\)
Bán kính hồ hình tròn tiếp xúc với các cạnh của khu vườn là: \[\frac{x}{2}\,\,({\rm{m}}).\]
Diện tích hồ hình tròn là: \[\pi \cdot {\left( {\frac{x}{2}} \right)^2} = \frac{{\pi {x^2}}}{4}\,\,\left( {{{\rm{m}}^2}} \right).\]
Vậy diện tích phần còn lại của khu vườn sau khi xây hồ là \[\frac{{\pi {x^2}}}{4}\,\,\left( {{{\rm{m}}^2}} \right).\]
b) Vì khu vườn hình chữ nhật có chiều dài gấp hai lần chiều rộng nên \(y = 2x.\)
Diện tích phần còn lại của khu vườn là \(77,76\,\,{{\rm{m}}^{\rm{2}}}\) nên ta có
\(xy - \frac{{\pi {x^2}}}{4} = 77,76\)
\(x \cdot 2x - \frac{{\pi {x^2}}}{4} = 77,76\)
\(8{x^2} - \pi {x^2} = 311,04\)
\({x^2}\left( {8 - \pi } \right) = 311,04\)
\({x^2}\left( {8 - \pi } \right) = 311,04\)
\({x^2} \approx 64\)
\(x = - 8\) (loại) hoặc \(x = 8\) (thỏa mãn).
Lời giải
Gọi \(x\,\,{\rm{(m}}\,{\rm{/}}\,{\rm{s)}}\) là tốc độ trượt ván của Bình và \(y\) (giây) là thời gian cuộc đua đã diễn ra \(\left( {x > 0\,;\,\,y > 0} \right).\)
Vì tốc độ trượt ván của An gấp 3 lần tốc độ trượt ván của Bình nên tốc độ trượt ván của An là \(3x\,\,{\rm{(m}}\,{\rm{/}}\,{\rm{s)}}{\rm{.}}\)
Vì tốc độ trượt ván của Bình gấp 3 lần tốc độ chạy bộ của An nên An chạy bộ với tốc độ là \(\frac{x}{3}\,\,{\rm{(m}}\,{\rm{/}}\,{\rm{s)}}{\rm{.}}\)
Thời gian An chạy bộ là \(y - 180\) (giây).
Quãng đường mà An trượt ván và chạy là \(3x \cdot 180 + \frac{x}{3} \cdot \left( {y - 180} \right)\,\,\left( {\rm{m}} \right).\)
Quãng đường mà Bình trượt ván là \(xy\,\,\left( {\rm{m}} \right).\)
Vì quãng đường của An và Bình đi là như nhau nên ta có phương trình:
\(3x \cdot 180 + \frac{x}{3} \cdot \left( {y - 180} \right) = xy\)
\(540x + \frac{{xy}}{3} - 60x = xy\)
\(480x = \frac{2}{3}xy\)
\(\frac{2}{3}x = 480\) (do \(x \ne 0)\)
\(y = 720\) (thỏa mãn).
Vậy thời gian cuộc đua diễn ra là 720 giây \[ = 12\] phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
|
(1,0 điểm) Bác Nam có một khối gỗ có dạng hình trụ với chiều cao là \(40\,\,{\rm{cm}}\) và đường kính đáy là \(20\,\,{\rm{cm}}{\rm{.}}\) Bác Nam muốn tiện khối gỗ này thành một vật trang trí có dạng hình nón có cùng chiều cao và bán kính với khối hình trụ ban đầu. |
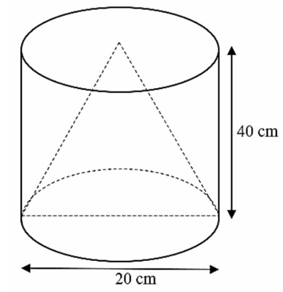 |
a) Tính thể tích phần gỗ bỏ đi khi thực hiện việc tiện gỗ hình trụ thành vật trang trí hình nón.
b) Sau khi hoàn thành sản phẩm, bác Nam dự tính phun sơn bề mặt bên ngoài của vật trang trí. Tính diện tích cần phải phun sơn (bao gồm cả mặt đáy).
(Các kết quả làm tròn chính xác đến hàng phần trăm của đơn vị)
Biết công thức tính thể tích khối trụ là \(V = \pi {R^2}h\) \((R\) là bán kính đáy, \(h\) là chiều cao); công thức tính thể tích hình nón là \(V = \frac{1}{3}\pi {R^2}h;\) công thức tính diện tích xung quanh hình nón là \(S = \pi Rl\) (\(l\) là độ dài đường sinh).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.