Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 19

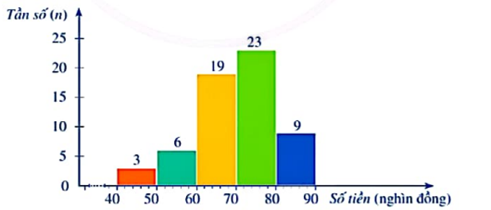
+ Tần số ghép nhóm của nhóm \[\left[ {40;50} \right)\] là \[3\].

+ Tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\] là: \[\frac{3}{{60}}.100\%  = 5\% \]

+ Tập hợp các kết quả có thể xảy ra khi thực hiện phép thử “Rút ngẫu nhiên một thẻ trong hộp”  là:              \[\left\{ {1;2;3;...;12} \right\}\] ; có \[12\] kết quả

+ Các kết quả thuận lợi cho biến cố \[M\]: “thẻ được rút ra ghi số chia hết cho \[3\]” là: \[\left\{ {3;6;9;12} \right\}\]

+ Xác suất của biến cố \[M\]là:  \[\frac{4}{{12}} = \frac{1}{3}\]

 1) Thay \[x = 9\] (thỏa mãn điều kiện) vào biểu thức \[B\] ta có:

\[B = \frac{{\sqrt 9  + 2}}{{\sqrt 9  - 2}} = \frac{{3 + 2}}{1} = 5\]

Vậy giá trị của \[B\] tại \[x = 9\] là \[5\].

2) \[A = \frac{3}{{\sqrt x  - 2}} - \frac{{\sqrt x  + 10}}{{x - 4}}\]

\[A = \frac{{3\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{\sqrt x  + 10}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\]

\[A = \frac{{3\left( {\sqrt x  + 2} \right) - \sqrt x  - 10}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\]

\[A = \frac{{2\sqrt x  - 4}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{2\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\]

\[A = \frac{2}{{\sqrt x  + 2}}\]

3) \[P = A.B = \frac{2}{{\sqrt x  + 2}}.\frac{{\sqrt x  + 2}}{{\sqrt x  - 2}} = \frac{2}{{\sqrt x  - 2}}\]

\[P \le  - 1 \Leftrightarrow \frac{2}{{\sqrt x  - 2}} \le  - 1 \Leftrightarrow \frac{2}{{\sqrt x  - 2}} + 1 \le 0 \Leftrightarrow \frac{{\sqrt x }}{{\sqrt x  - 2}} \le 0\]

* Nếu \[\frac{{\sqrt x }}{{\sqrt x  - 2}} = 0\] thì \[\sqrt x  = 0 \Leftrightarrow x = 0\] (không thỏa mãn đk x là số nguyên tố)

* Nếu \[\frac{{\sqrt x }}{{\sqrt x  - 2}} < 0\] thì ta có hai trường hợp sau:

\[TH1:\left\{ \begin{array}{l}\sqrt x  > 0\\\sqrt x  - 2 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x < 4\end{array} \right. \Leftrightarrow 0 < x < 4\](thỏa mãn đk \[x \ge 0;x \ne 4\])  mà \[x\] là số nguyên tố nên \[x = 2;x = 3\]

\[TH2:\left\{ \begin{array}{l}\sqrt x  < 0\\\sqrt x  - 2 > 0\end{array} \right. \Leftrightarrow x \in \emptyset \]

Vậy \[x = 2;x = 3\] thì thỏa mãn đề bài

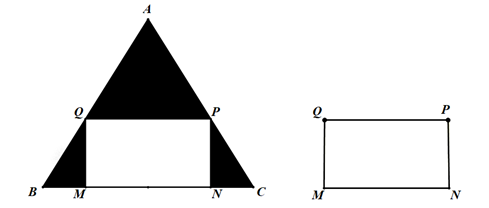
Gọi độ dài đoạn \[MB\] là \[x(cm)\], ta có:

Độ dài đoạn \[NC\] là \[x(cm)\]

Độ dài đoạn \[MN\] là \[20 - x - x = 20 - 2x(cm)\]

Tam giác \[BQM\] vuông tại \[M\] có:

                        \[\tan B = \tan {60^0} = \frac{{QM}}{{BM}} = \frac{{QM}}{x}\]

                           \[QM = x.\tan {60^0} = x.\sqrt 3 \]

Diện tích hình chữ nhật \[MNPQ\] là: \[S = MN.QM = (20 - 2x).x\sqrt 3 \]

Áp dụng bất đẳng thức Cauchy ta có: \[S = (20 - 2x).x\sqrt 3  = 2\sqrt 3 (10 - x).x \le 2\sqrt 3 {\left( {\frac{{10 - x + x}}{2}} \right)^2}\]

                                                                     \[S \le 2\sqrt 3 .25 = 50\sqrt 3 \]

Dấu bằng xảy ra khi \[10 - x = x\] nên \[x = 5\]

Vậy \[MB = 5cm\] để hình chữ nhật \[MNPQ\] có diện tích lớn nhất.

Gọi khối lượng dung dịch \[HCl\] \[10\% \] là \[x{\rm{ }}(gam,x > 0)\]

Gọi khối lượng dung dịch \[HCl\] \[25\% \] là \[y{\rm{ }}(gam,y > 0)\]

Vì tổng khối lượng hai dung dịch là \[500\] \[gam\] nên ta có phương trình:

\[x + y = 500{\rm{ }}(1)\]

Vì dung dịch tạo thành là \[HCl\] \[16\% \] nên ta có phương trình:

\[10\% x + 25\% y = 16\% .500{\rm{ }}(2)\]

Từ \[(1);{\rm{ }}(2)\] ta có hệ phương trình:

\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\10\% x + 25\% y = 16\% .500{\rm{ }}\end{array} \right.\]

\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\0,1x + 0,25y = 80{\rm{ }}\end{array} \right.\]

\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\x + 2,5y = 800{\rm{ }}\end{array} \right.\]

\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\ - 1,5y =  - 300{\rm{ }}\end{array} \right.\]

 \[\left\{ \begin{array}{l}x = 300{\rm{ }}(tm){\rm{ }}\\y = 200{\rm{ }}(tm){\rm{ }}\end{array} \right.\]

Vậy Bình cần dùng \[300\] \[gam\] dung dịch \[HCl\] \[10\% \] và \[200\]\[gam\] dung dịch \[HCl\] \[25\% \]