Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 48

Nhóm \[\left[ {40\,\,;\,\,60} \right)\] có tần số tương đối là \[\frac{{11}}{{36}} \approx 30,6\% \]

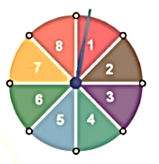
Ta có\(\Omega  = \left\{ {1\,;\,2\,;\,3\,;\,4\,;\,5\,;\,6\,;\,7\,;\,\left. 8 \right\}} \right.\), có 8 phần tử.

 Các kết quả thuận lợi cho biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của \[8\]”

là: \[1\,;\,2\,;\,4\,;\,8\]

\( \Rightarrow \)Xác suất của biến cố: “Mũi tên chỉ vào hình quạt ghi số là ước của \[8\]” là: \(\frac{4}{8} = \frac{1}{2}\)

1) Tính giá trị của biểu thức \(B\) với \(x = 25\).

Với \(x = 25\) (thỏa mãn điều kiện) thay vào biểu thức \(B\) ta có:

\(B = \frac{{\sqrt {25}  + 3}}{{\sqrt {25}  + 1}} = \frac{{5 + 3}}{{5 + 1}} = \frac{8}{6} = \frac{4}{3}\).

Vậy \(B = \frac{4}{3}\) khi \(x = 25\).

2) Chứng minh \(A = \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}\).

Ta có:  \(A = \frac{{\sqrt x }}{{\sqrt x  - 1}} + \frac{1}{{\sqrt x  + 2}} - \frac{{3\sqrt x }}{{x + \sqrt x  - 2}}\)

\( = \frac{{\sqrt x }}{{\sqrt x  - 1}} + \frac{1}{{\sqrt x  + 2}} - \frac{{3\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

\( = \frac{{\sqrt x \left( {\sqrt x  + 2} \right) + \left( {\sqrt x  - 1} \right) - 3\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{x - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

\( = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}\)

Vậy \(A = \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}\)với \(x \ge 0\); \(x \ne 1\).

3) Tìm \(x\) để biểu thức \(S = A.B\) đạt giá trị lớn nhất.

Với \(x \ge 0\); \(x \ne 1\).

Ta có: \(S = A.B = \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}.\frac{{\sqrt x  + 3}}{{\sqrt x  + 1}} = \frac{{\sqrt x  + 3}}{{\sqrt x  + 2}} = 1 + \frac{1}{{\sqrt x  + 2}}\)

Ta có: \(x \ge 0\)\( \Rightarrow \sqrt x  + 2 \ge 2\)\( \Rightarrow \frac{1}{{\sqrt x  + 2}} \le \frac{1}{2}\)\( \Rightarrow 1 + \frac{1}{{\sqrt x  + 2}} \le 1 + \frac{1}{2} = \frac{3}{2}\)

Dấu  xảy ra khi \(x = 0\) (thỏa mãn điều kiện).

Vậy GTLN của \(S\) là \(\frac{3}{2}\) khi \(x = 0\).

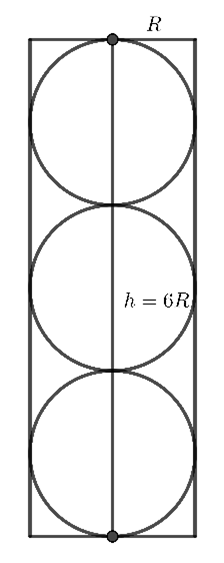
Đặt \(h,\,\,R\) lần lượt là đường cao và bán kính hình tròn đáy của hộp đựng bóng tennis.

Dễ thấy mỗi quả bóng tennis có cùng bán kính \(R\) với hình tròn đáy của hộp đựng bóng tennis và \(h = 6R\).

Do đó ta có:

Tổng thể tích của ba quả bóng là \({V_1} = 3.\frac{4}{3}\pi {R^3} = 4\pi {R^3}\);

Thể tích của hình trụ (hộp đựng bóng) là \({V_0} = \pi {R^2}h = 6\pi {R^3}\);

Thể tích phần còn trống của hộp đựng bóng là \({V_2} = {V_0} - {V_1} = 2\pi {R^3}\).

Khi đó tỉ lệ phần không gian còn trống so với hộp đựng bóng là \(\frac{{{V_2}}}{{{V_0}}} = \frac{1}{3} \approx 0,33 \approx 33\% \).

Gọi \(x\) ( triệu đồng) là giá tiền một tủ lạnh khi chưa giảm giá \((x > 0)\)

Gọi \(y\) ( triệu đồng) là giá tiền một máy giặt khi chưa giảm giá \((y > 0)\)

Giá niêm yết hai món đồ trên là \(25,4\) triệu nên có phương trình:

\(x + y = 25,4\)

Giá bán hai món đồ trên  sau khi giảm giá là \(16,77\)triệu nên có phương trình 

\(\left( {100\%  - 40\% } \right).x + \left( {100\%  - 25\% } \right).y = 16,77\)

Giải hệ phương trình \[\left\{ \begin{array}{l}x + y = 25,4\\\frac{3}{5}x + \frac{3}{4}y = 16,77\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}x = 15,2(t/m)\\y = 10,2(t/m)\end{array} \right.\]

Vậy giá một tủ lạnh chưa giảm giá là \(15,2\) triệu đồng

Giá một máy giặt chưa giảm giá là \(10,2\)triệu đồng