(1,5 điểm) Cho hai biểu thức \(A = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{1}{{\sqrt x + 2}} - \frac{{3\sqrt x }}{{x + \sqrt x - 2}}\) và \(B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}}\) với \(x \ge 0\); \(x \ne 1\).
1) Tính giá trị của biểu thức \(B\) với \(x = 25\).
2) Chứng minh \(A = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\).
3) Tìm \(x\) để biểu thức \(S = A.B\) đạt giá trị lớn nhất.
(1,5 điểm) Cho hai biểu thức \(A = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{1}{{\sqrt x + 2}} - \frac{{3\sqrt x }}{{x + \sqrt x - 2}}\) và \(B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}}\) với \(x \ge 0\); \(x \ne 1\).
1) Tính giá trị của biểu thức \(B\) với \(x = 25\).
2) Chứng minh \(A = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\).
3) Tìm \(x\) để biểu thức \(S = A.B\) đạt giá trị lớn nhất.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 48 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Tính giá trị của biểu thức \(B\) với \(x = 25\).
Với \(x = 25\) (thỏa mãn điều kiện) thay vào biểu thức \(B\) ta có:
\(B = \frac{{\sqrt {25} + 3}}{{\sqrt {25} + 1}} = \frac{{5 + 3}}{{5 + 1}} = \frac{8}{6} = \frac{4}{3}\).
Vậy \(B = \frac{4}{3}\) khi \(x = 25\).
2) Chứng minh \(A = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\).
Ta có: \(A = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{1}{{\sqrt x + 2}} - \frac{{3\sqrt x }}{{x + \sqrt x - 2}}\)
\( = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{1}{{\sqrt x + 2}} - \frac{{3\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{\sqrt x \left( {\sqrt x + 2} \right) + \left( {\sqrt x - 1} \right) - 3\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \frac{{x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\)
Vậy \(A = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\)với \(x \ge 0\); \(x \ne 1\).
3) Tìm \(x\) để biểu thức \(S = A.B\) đạt giá trị lớn nhất.
Với \(x \ge 0\); \(x \ne 1\).
Ta có: \(S = A.B = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}.\frac{{\sqrt x + 3}}{{\sqrt x + 1}} = \frac{{\sqrt x + 3}}{{\sqrt x + 2}} = 1 + \frac{1}{{\sqrt x + 2}}\)
Ta có: \(x \ge 0\)\( \Rightarrow \sqrt x + 2 \ge 2\)\( \Rightarrow \frac{1}{{\sqrt x + 2}} \le \frac{1}{2}\)\( \Rightarrow 1 + \frac{1}{{\sqrt x + 2}} \le 1 + \frac{1}{2} = \frac{3}{2}\)
Dấu xảy ra khi \(x = 0\) (thỏa mãn điều kiện).
Vậy GTLN của \(S\) là \(\frac{3}{2}\) khi \(x = 0\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
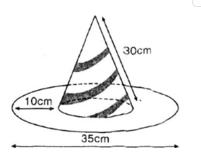
a) Bán kính đường tròn đáy của hình nón: \[r = \frac{{35 - 2.10}}{2} = 7,5\,({\rm{cm}})\]
Chiều cao của cái mũ: \[h = \sqrt {{{30}^2} - {{7,5}^2}} \approx 29(cm)\]
Tính thể tích của cái mũ: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.7,5^2}.29 = 543,75\pi \approx 1708(c{m^3})\]
b) Diện tích giấy làm nên cái mũ là tổng diện tích xung quanh của hình nón và diện tích vành nón.
Diện tích xung quanh hình nón: \[Sxq\; = \pi .r.l = \pi .7,5.30 = 225\pi {\rm{ }}({\rm{c}}{{\rm{m}}^2})\]
Diện tích vành nón (hình vành khăn): \[{S_{vk}} = \pi .{\left( {\frac{{35}}{2}} \right)^2} - \pi {.7,5^2} = 250\pi \,({\rm{c}}{{\rm{m}}^2})\]
Diện tích tích giấy làm nên cái mũ : \[S = 225\pi + 250\pi = 475\pi {\rm{ }} \approx {\rm{ }}1492{\rm{ (c}}{{\rm{m}}^{\rm{2}}})\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Nhóm \[\left[ {40\,\,;\,\,60} \right)\] có tần số tương đối là \[\frac{{11}}{{36}} \approx 30,6\% \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập