Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 4

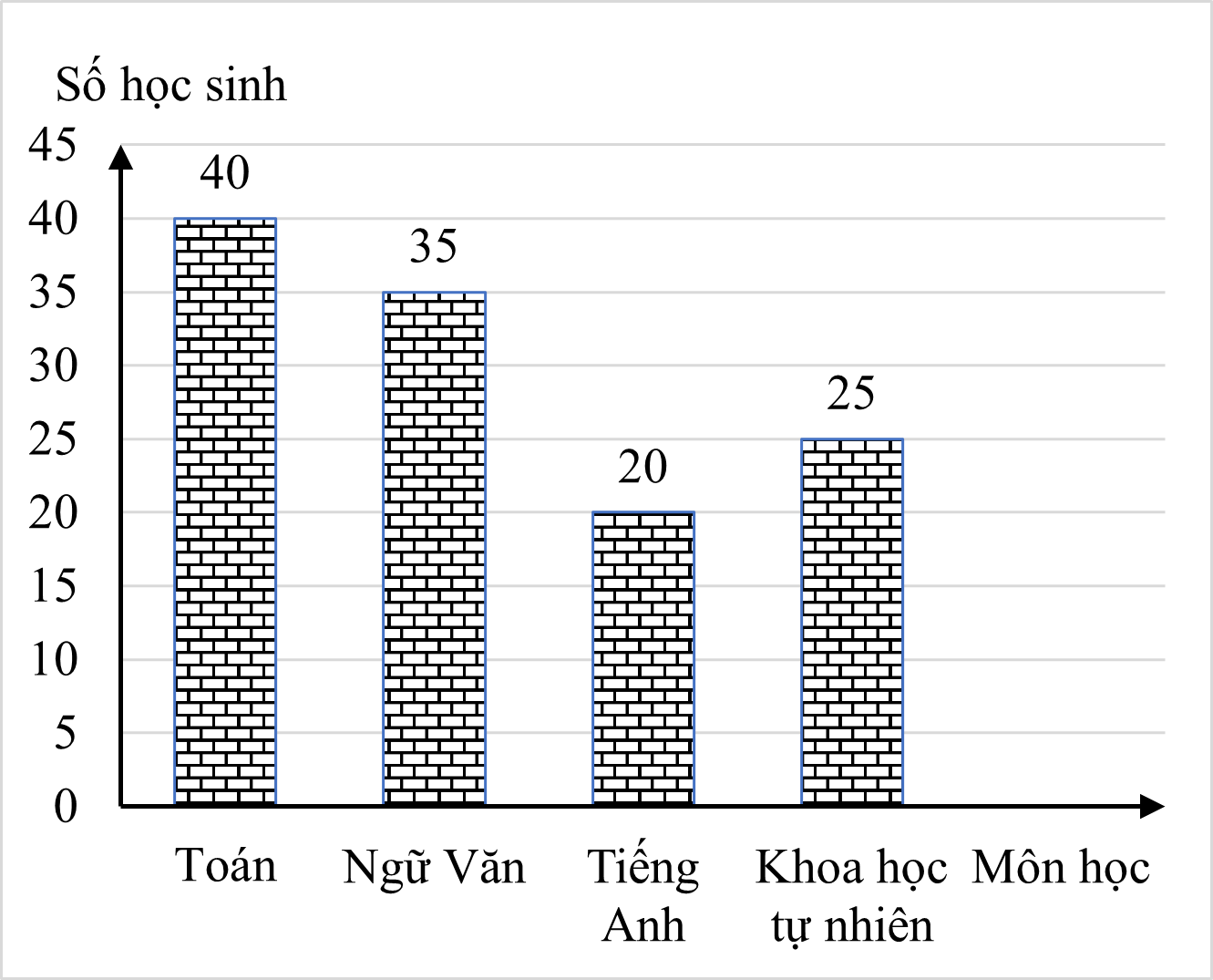
Quan sát biểu đồ, ta có:

Tổng số học sinh khối \(9\) là: \(40 + 35 + 20 + 25 = 120\) học sinh. Vậy \(N = 120\).

Bảng tần số:

Tần số tương đối của số học sinh yêu thích các môn Toán, Ngữ Văn, Tiếng Anh, Khoa học tự nhiên lần lượt là:

\({f_1} = \frac{{40}}{{120}}\,\, \cdot \,\,100\%  \approx 33,33\% \); \({f_2} = \frac{{35}}{{120}}\,\, \cdot \,\,100\%  \approx 29,17\% \);

 \({f_3} = \frac{{20}}{{120}}\,\, \cdot \,\,100\%  \approx 16,67\% \); \({f_4} = \frac{{25}}{{120}}\,\, \cdot \,\,100\%  \approx 20,83\% \).

Bảng tần số tương đối:

Điều kiện \(x \ge 0\), \(x \ne 4\).

 Ta có: \(x =  - \frac{3}{2}\,\, \cdot \,\,\sqrt[3]{{\frac{{ - 8}}{{27}}}} =  - \frac{3}{2}\,\, \cdot \,\,\sqrt[3]{{{{\left( {\frac{{ - 2}}{3}} \right)}^3}}} =  - \frac{3}{2}\,\, \cdot \,\,\frac{{ - 2}}{3} = 1\).

Thay \(x = 1\) (thỏa mãn điều kiện) vào \(A\) ta được: \(A = \frac{{\sqrt 1  - 2}}{{\sqrt 1  + 9}} = \frac{{1 - 2}}{{1 + 9}} = \frac{{ - 1}}{{10}}\).

Vậy \(A = \frac{{ - 1}}{{10}}\) khi \(x =  - \frac{3}{2}\,\, \cdot \,\,\sqrt[3]{{\frac{{ - 8}}{{27}}}}\).

Ta có: \(B = \frac{3}{{\sqrt x  + 2}} - \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{9\sqrt x  - 10}}{{4 - x}}\)

                  \( = \frac{{3\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} + \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{9\sqrt x  - 10}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)

                 \( = \frac{{3\sqrt x  - 6 + x + 2\sqrt x  - 9\sqrt x  + 10}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\)

                 \( = \frac{{x - 4\sqrt x  + 4}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)

                 \( = \frac{{{{\left( {\sqrt x  - 2} \right)}^2}}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)

                \( = \frac{{\sqrt x  - 2}}{{\sqrt x  + 2}}\).

Vậy \(B = \frac{{\sqrt x  - 2}}{{\sqrt x  + 2}}\) với \(x \ge 0\), \(x \ne 4\).

Ta có: \(P = B:A = \frac{{\sqrt x  - 2}}{{\sqrt x  + 2}}:\frac{{\sqrt x  - 2}}{{\sqrt x  + 9}}\)\( = \frac{{\sqrt x  - 2}}{{\sqrt x  + 2}}\,\, \cdot \,\,\frac{{\sqrt x  + 9}}{{\sqrt x  - 2}}\)\( = \frac{{\sqrt x  + 9}}{{\sqrt x  + 2}}\)\( = 1 + \frac{7}{{\sqrt x  + 2}}\)

Vì \(7 > 0\), \(\sqrt x  + 2 > 0\) nên \(\frac{7}{{\sqrt x  + 2}} > 0\).

Do \(\sqrt x  \ge 0\) nên \(\sqrt x  + 2 \ge 2\), suy ra \(\frac{7}{{\sqrt x  + 2}} \le \frac{7}{2}\)

Do đó \(0 < \frac{7}{{\sqrt x  + 2}} \le \frac{7}{2}\), suy ra \(1 < \frac{7}{{\sqrt x  + 2}} + 1 \le \frac{7}{2} + 1\) hay \(1 < P < \frac{9}{2}\).

Mà \(P\) là số chính phương nên \(P = 4\).

Với \(P = 4\), ta có \(\frac{7}{{\sqrt x  + 2}} = 3\)

                           \(\sqrt x  + 2 = \frac{7}{3}\)

                                   \(x = \frac{1}{9}\) (thỏa mãn điều kiện).

            Vậy \(x = \frac{1}{9}\)thì thoả mãn đề bài.