Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Bình Định có đáp án

1. Giải hệ phương trình

\(\left\{ {\begin{array}{*{20}{l}}{5x + 3y = 1}\\{x - 3y = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{6x = 6}\\{x - 3y = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{1 - 3y = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = \frac{{ - 4}}{3}}\end{array}} \right.} \right.} \right.} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(({\rm{x}};{\rm{y}}) = \left( {1;\frac{{ - 4}}{3}} \right)\)

2. a) Với \(x \ge 0;x \ne 16\) ta có:

\(\begin{array}{l}P = \frac{{\sqrt x }}{{\sqrt x  + 4}} + \frac{{3\sqrt x }}{{\sqrt x  - 4}} - \frac{{4x + 32}}{{x - 16}} = \frac{{\sqrt x \left( {\sqrt x  - 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} + \frac{{3\sqrt x \left( {\sqrt x  + 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} - \frac{{4x + 32}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}}\\\,\,\,\,\, = \frac{{x - 4\sqrt x  + 3x + 12\sqrt x  - 4x - 32}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} = \frac{{8\sqrt x  - 32}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} = \frac{{8\left( {\sqrt x  - 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} = \frac{8}{{\sqrt x  + 4}}.\end{array}\)

\(b)\) Với \(x \ge 0;x \ne 16\)ta có: \(\sqrt x  + 4 \ge 4\). Suy ra: \(P = \frac{8}{{\sqrt x  + 4}} \le \frac{8}{4} = 2\)

Dấu "=" xảy ra khi \(x = 0\). Vậy GTLN của \(P\) là 2 khi \(x = 0\)

1. Phương trình có \(\Delta  = {({\rm{m}} + 3)^2} - 4 \cdot \left( {\frac{1}{4}\;{{\rm{m}}^2} + 1} \right) = {{\rm{m}}^2} + 6\;{\rm{m}} + 9 - {{\rm{m}}^2} - 4 = 6\;{\rm{m}} + 5\)

Phương trình có hai nghiệm phân biệt \({{\rm{x}}_1},{{\rm{x}}_2} \Leftrightarrow 6\;{\rm{m}} + 5 > 0 \Leftrightarrow {\rm{m}} > \frac{{ - 5}}{6}\)

Theo hệ thức Vi - ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m + 3}\\{{x_1} \cdot {x_2} = \frac{1}{4}{m^2} + 1}\end{array}} \right.\)

Theo đề ta có: \(2{\left( {{{\rm{x}}_1} + {{\rm{x}}_2}} \right)^2} - 8{{\rm{x}}_1}{{\rm{x}}_2} = 34\)

\( \Leftrightarrow 2.{({\rm{m}} + 3)^2} - 8.\left( {\frac{1}{4}\;{{\rm{m}}^2} + 1} \right) = 34 \Leftrightarrow 2\;{{\rm{m}}^2} + 12\;{\rm{m}} + 18 - 2\;{{\rm{m}}^2} - 8 - 34 = 0\)

\( \Leftrightarrow 12\;{\rm{m}} - 24 = 0 \Leftrightarrow {\rm{m}} = 2\) (TMĐK). Vậy \({\rm{m}} = 2\) là giá trị cần tìm.

2. Vì \(A( - 1;5) \in (d):y = ax - 4\) nên: \(5 = {\rm{a}} \cdot ( - 1) - 4 \Leftrightarrow 5 =  - {\rm{a}} - 4 \Leftrightarrow {\rm{a}} =  - 9\)

Vậy a \( =  - 9\).

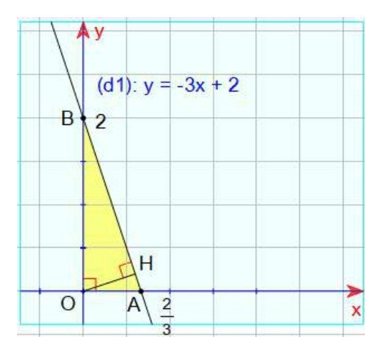
b) Tọa độ giao điểm của \(\left( {{{\rm{d}}_1}} \right)\) với trục hoành là \({\rm{A}}\left( {\frac{2}{3};0} \right)\)

Tọa độ giao điểm của \(\left( {{{\rm{d}}_1}} \right)\) với trục tung là \({\rm{B}}(0;2)\)

Ta có: \({\rm{OA}} = \left| {\frac{2}{3}} \right| = \frac{2}{3}(\) đvđd) \({\rm{OB}} = |2| = 2\)(đvđd)

\({\rm{AB}} = \sqrt {{\rm{O}}{{\rm{A}}^2} + {\rm{O}}{{\rm{B}}^2}}  = \sqrt {{{\left( {\frac{2}{3}} \right)}^2} + {2^2}}  = \frac{{2\sqrt {10} }}{3}({\rm{dvdd}})\)

Diện tích tam giác \({\rm{OAB}}\) là:

\({{\rm{S}}_{{\rm{OAB}}}} = \frac{1}{2} \cdot {\rm{OA}} \cdot {\rm{OB}} = \frac{1}{2} \cdot \frac{2}{3} \cdot 2 = \frac{2}{3}({\rm{dvdt}})\)

Khoảng cách từ gốc tọa độ \({\rm{O}}\) đến \(\left( {{{\rm{d}}_1}} \right)\) là:

\(\frac{{2.{{\rm{S}}_{{\rm{OAB}}}}}}{{{\rm{AB}}}} = \frac{{2 \cdot \frac{2}{3}}}{{\frac{{2\sqrt {10} }}{3}}} = \frac{{\sqrt {10} }}{5}\) (đvđd)

Gọi \({\rm{x}},{\rm{y}}\) (thí sinh) lần lượt là số thí sinh dự thi của hai trường \({\rm{A}}\) và \({\rm{B}}\).

ĐK: \(x\), y nguyên dương; \(x,y < 380\).

Vì số thí sinh dự thi của cả hai trường là 380 thí sinh nên ta có phương trình: \({\rm{x}} + {\rm{y}} = 380\)

Số thí sinh trúng tuyển của trường \({\rm{A}}\) là: \(55\% x = 0,55x\) (thí sinh)

Số thí sinh trúng tuyển của trường \({\rm{B}}\) là: \(45\% y = 0,45y\) (thí sinh)

Ta có phương trình: \(0,55x + 0,45y = 191\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 380}\\{0,55x + 0,45y = 180}\end{array}} \right.\)

Giải hệ phương trình ta được: \(\left\{ {\begin{array}{*{20}{l}}{x = 200}\\{y = 180}\end{array}} \right.\) (TMĐK)

Vậy số thí sinh dự thi của trường \({\rm{A}}\) là 200 thí sinh

Số thí sinh dự thi của trường \(B\) là 180 thí sinh.

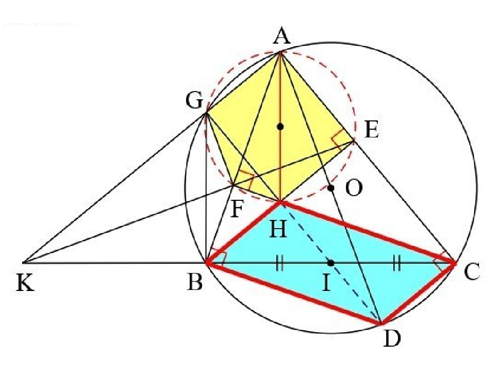
1) Ta có: \(\widehat {BEC} = \widehat {BFC} = {90^^\circ }\) nên \({\rm{B}},{\rm{F}},{\rm{E}},{\rm{C}}\) cùng thuộc đường tròn đường kính \({\rm{BC}}\).

Suy ra tứ giác \({\rm{BFEC}}\) nội tiếp đường tròn đường kính \({\rm{BC}}\).

2) Xét \(\Delta KBF\) và \(\Delta KEC\) có:

\(\widehat {{\rm{KFB}}} = \widehat {{\rm{KCE}}}\) (vì cùng bù với góc \({\rm{BFE}})\)

\(\widehat {{\rm{BKF}}}\) : chung

Do đó:

Suy ra: \(\frac{{{\rm{KB}}}}{{{\rm{KE}}}} = \frac{{{\rm{KF}}}}{{{\rm{KC}}}} \Rightarrow {\rm{KB}}{\rm{.KC}} = {\rm{KF}}.{\rm{KE}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)        (1)

3) Ta chứng minh được (g.g)

Suy ra:\(\frac{{{\rm{KB}}}}{{{\rm{KA}}}} = \frac{{{\rm{KG}}}}{{{\rm{KC}}}} \Rightarrow {\rm{KB}}{\rm{.KC}} = {\rm{KA}}{\rm{.KG}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)                (2)

Từ (1), (2) suy ra: \({\rm{KA}}{\rm{.KG}} = {\rm{KE}}{\rm{.KF}}\,\,\,\,\,\,\,\,\,\,\,\)

Xét \(\Delta {\rm{KGF}}\) và \(\Delta {\rm{KEA}}\) có: \(\frac{{{\rm{KG}}}}{{{\rm{KE}}}} = \frac{{{\rm{KF}}}}{{{\rm{KA}}}}\) (vì \({\rm{KA}}{\rm{.KG}} = {\rm{KE}}{\rm{.KF}}\)); \(\widehat {{\rm{GKF}}}\) : chung

Do đó: (c.g.c)

Suy ra: \(\widehat {{\rm{KGF}}} = \widehat {{\rm{KEA}}} \Rightarrow \) Tứ giác AGFE nội tiếp                              (3)

Tứ giác \({\rm{AEHF}}\) nội tiếp (vì \(\widehat {{\rm{AEH}}} + \widehat {{\rm{AFH}}} = {180^^\circ }\))                             (4)

Từ (3) và (4) suy ra 5 điểm: A, G, F, H, E cùng thuộc đường tròn đường kính \({\rm{AH}}\).

4) Kẻ đường kính \({\rm{AD}}\) của đường tròn \(({\rm{O}})\). Khi đó: \({\rm{BH}}//{\rm{CD}}\) (vì cùng vuông góc với \({\rm{AC}}\)) \({\rm{CH}}//{\rm{BD}}\) (vì cùng vuông góc với \({\rm{AB}}\)). Do đó tứ giác \({\rm{BHCD}}\) là hình bình hành.

Lại có \({\rm{I}}\) là trung điểm của đường chéo \({\rm{BC}}\) nên I là trung điểm của đường chéo \({\rm{HD}}\)

Suy ra: H, I, D thẳng hàng                                                                 (5)

Ta có: \(\widehat {{\rm{AGD}}} = {90^^\circ }\) (vì nội tiếp chắn nửa đường tròn)                       (6)

\(\widehat {AGH} = \widehat {AFH} = {90^^\circ }\) (vì nội tiếp cùng chắn cung \({\rm{AH}}\))                      (7)

Từ (5), (6) và (7) suy ra: \({\rm{H}},{\rm{G}},{\rm{I}}\) thẳng hàng. Vậy \({\rm{HI}}\) vuông góc với \({\rm{AK}}\).

Cách 1: Ta có:

\(\begin{array}{l}\frac{a}{{a + \sqrt {2024a + bc} }} = \frac{a}{{a + \sqrt {(a + b + c)a + bc} }} = \frac{a}{{a + \sqrt {(a + b)(a + c)} }} = \frac{{a(\sqrt {(a + b)(a + c)}  - a)}}{{(a + \sqrt {(a + b)(a + c)} ) \cdot (\sqrt {(a + b)(a + c)}  - a)}}\,\\ = \frac{{a(\sqrt {(a + b)(a + c)}  - a)}}{{(a + b)(a + c) - {a^2}}} = \frac{{a(\sqrt {(a + b)(a + c)}  - a)}}{{ab + bc + ac}}\end{array}\)

Áp dụng Bất đẳng thức Cô-si cho hai số dương \({\rm{a}} + {\rm{b}}\) và \({\rm{a}} + {\rm{c}}\), ta có :

\(\sqrt {(a + b)(a + c)}  \le \frac{{a + b + a + c}}{2} = \frac{{2a + b + c}}{2}\)

Do đó: \(\frac{a}{{a + \sqrt {2024a + bc} }} = \frac{{a(\sqrt {(a + b)(a + c)}  - a)}}{{ab + bc + ac}} \le \frac{{a\left( {\frac{{2a + b + c}}{2} - a} \right)}}{{ab + bc + ac}} = \frac{{ab + ac}}{{2(ab + bc + ac)}}\)

Tương tự: \(\frac{b}{{b + \sqrt {2024b + ca} }} \le \frac{{bc + ab}}{{2(ab + bc + ac)}}\)

                  \(\frac{c}{{c + \sqrt {2024c + ab} }} \le \frac{{ac + bc}}{{2(ab + bc + ac)}}\)

Từ (1), (2) và (3) suy ra: \({\rm{P}} \le \frac{{2(ab + bc + ca)}}{{2(ab + bc + ca)}} = 1\)

Dấu "=" xảy ra khi \(\left\{ {\begin{array}{*{20}{l}}{a = b = c}\\{a + b + c = 2024}\end{array} \Leftrightarrow a = b = c = \frac{{2024}}{3}} \right.\)

Vậy GTLN của P là 1 khi \(a = b = c = \frac{{2024}}{3}\)

Cách 2: Ta có 2024a \( + {\rm{bc}} = ({\rm{a}} + {\rm{b}} + {\rm{c}}) \cdot {\rm{a}} + {\rm{bc}} = {{\rm{a}}^2} + {\rm{ab}} + {\rm{ac}} + {\rm{bc}} = ({\rm{a}} + {\rm{b}})({\rm{a}} + {\rm{c}})\)

Tương tự: \(\quad 2024b + ca = (b + c)(b + a)\)

\(2024c + ab = (c + a)(c + b)\)

Do đó \({\rm{P}} = \frac{{\rm{a}}}{{{\rm{a}} + \sqrt {(a + b)(a + c)} }} + \frac{{\rm{b}}}{{{\rm{b}} + \sqrt {(a + b)(a + c)} }} + \frac{{\rm{c}}}{{{\rm{c}} + \sqrt {({\rm{a}} + {\rm{c}})(b + c)} }}\)

Áp dụng bất đẳng thức Bunhiacopski ta có:

\(\sqrt {(a + b)(c + a)}  = \sqrt {\left( {{{(\sqrt a )}^2} + {{(\sqrt b )}^2}} \right) \cdot \left( {{{(\sqrt c )}^2} + {{(\sqrt a )}^2}} \right)}  \ge \sqrt {ac}  + \sqrt {ab} \)

Suy ra \(\frac{a}{{a + \sqrt {(a + b)(a + c)} }} \le \frac{a}{{a + \sqrt {ac}  + \sqrt {ab} }} = \frac{{\sqrt a }}{{\sqrt a  + \sqrt b  + \sqrt c }}\)

Tương tự \(\frac{b}{{b + \sqrt {(a + b)(a + c)} }} \le \frac{{\sqrt b }}{{\sqrt a  + \sqrt b  + \sqrt c }};\frac{c}{{c + \sqrt {(a + c)(b + c)} }} \le \frac{{\sqrt c }}{{\sqrt a  + \sqrt b  + \sqrt c }}\)

Do đó \({\rm{P}} \le \frac{{\sqrt {\rm{a}}  + \sqrt {\rm{b}}  + \sqrt {\rm{c}} }}{{\sqrt {\rm{a}}  + \sqrt {\rm{b}}  + \sqrt {\rm{c}} }} = 1\)

Dấu "=" xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b + c = 2024}\\{a = b = c}\end{array} \Leftrightarrow a = b = c = \frac{{2024}}{3}} \right.\).