Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 7

1) Số học sinh bình chọn cho Tuấn là \(\frac{{500 \cdot 30\% }}{{100\% }} = 150\) (học sinh)

Số học sinh bình chọn cho Trường là \(\frac{{500 \cdot 25\% }}{{100\% }} = 125\) (học sinh)

Số học sinh bình chọn cho An là \(\frac{{500 \cdot 10\% }}{{100\% }} = 50\) (học sinh)

Số học sinh bình chọn cho Linh là \(\frac{{500 \cdot 35\% }}{{100\% }} = 175\) (học sinh)

Ta có bảng tần số

 2) Tổng số học sinh bình chọn cho Tuấn và Trường là \(150 + 125 = 275\)

Xác suất cầu thủ được chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường có tên bắt đầu bởi chữ cái “\(T\)” là \(\frac{{275}}{{500}} = 0,55\).

Vậy xác suất tìm được là \(0,55\)

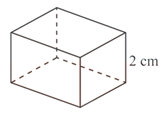
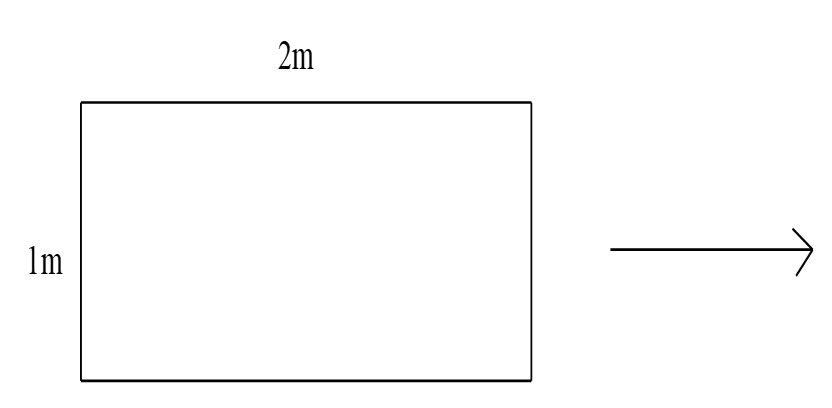
Gọi chiều rộng của đáy hộp là \(x\)( \(x > 0\), cm).

                 Ta có chiều dài của hộp là \(\frac{{500}}{{2x}}\) (cm)

                 Ta có diện tích toàn phần của chiếc hộp là

                 \(S = 2x \cdot \frac{{500}}{{2x}} + 2\left( {x + \frac{{500}}{{2x}}} \right) \cdot 2 = 500 + 2x + \frac{{250}}{x}\) (cm2)

                 Áp dụng bất đẳng thức Cauchy cho hai số thực dương \(2x\) và \(\frac{{250}}{x}\), ta có

                 \(2x + \frac{{250}}{x} \ge 2\sqrt {2x \cdot \frac{{250}}{x}}  = 20\sqrt 5 \)

                 Từ đó  \(S \ge 500 + 20\sqrt 5 \,\,\) (cm2)

                 Dấu  xảy ra khi và chỉ khi \(2x = \frac{{250}}{x}\) hay \({x^2} = \frac{{250}}{2} = 125\)

                 Suy ra \(x = 5\sqrt 5 \)cm, từ đó \(\frac{{250}}{{5\sqrt 5 }} = 10\sqrt 5 \)cm.

                 Vậy chiều rộng của hộp là \(5\sqrt 5 \)cm, chiều dài là \(10\sqrt 5 \)cm.

            Chứng minh bổ sung Bất đẳng thức Cauchy

            Xét hai số thực dương \(a\), \(b\)ta có \(\frac{{a + b}}{2} \ge \sqrt {ab} \).

            Thật vậy, vì \(a\), \(b\) là các số thực dương nên

            Từ \(\frac{{a + b}}{2} \ge \sqrt {ab} \), suy ra \(a + b \ge 2\sqrt {ab} \)

            Hay \({\left( {\sqrt a } \right)^2} + {\left( {\sqrt b } \right)^2} - 2\sqrt {ab}  \ge 0\)

                    \({\left( {\sqrt a  - \sqrt b } \right)^2} \ge 0\) (luôn đúng)

            Vậy với hai số thực dương \(a\), \(b\) bất kỳ ta có \(\frac{{a + b}}{2} \ge \sqrt {ab} \).

            Dấu “\( = \)” xảy ra khi \(a = b\)

Thay \(x = 36\)(tmđk) vào \(A\) ta được \(A = \frac{{36 - 5}}{{\sqrt {36} }} = \frac{{31}}{6}\)

Vậy \(A = \frac{{31}}{6}\)khi \(x = 36\)

\(B = \frac{{2x + 2\sqrt x }}{{x - 1}} - \frac{{\sqrt x }}{{\sqrt x  - 1}}\) với \(x > 0,x \ne 1\).

\[B = \frac{{2x + 2\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} - \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\]

\[B = \frac{{x + \sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} = \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\]

\[B = \frac{{\sqrt x }}{{\sqrt x  - 1}}\]

Vậy \[B = \frac{{\sqrt x }}{{\sqrt x  - 1}}\] , \(x > 0,x \ne 1\)

Tìm tất cả giá trị nguyên của \(x\) để biểu thức \(P = AB\) có giá trị nguyên

\[P = \frac{{x - 5}}{{\sqrt x  - 1}}\]

\[P = \frac{{x - 5}}{{\sqrt x  - 1}} = 0 \Rightarrow x = 5\,\left( {tm} \right)\]

\[P \ne 0,x \in Z,\sqrt x  \in I \Rightarrow P \notin Z\]

\[P = \sqrt x  + 1 - \frac{4}{{\sqrt x  - 1}} \ne 0,x \in Z,\sqrt x  \in Z \Rightarrow \sqrt x  - 1 \in U\left( 4 \right)\]

\[x \in \left\{ {4;9;25} \right\}\] (tmđk)

Vậy \[x \in \left\{ {4;5;9;25} \right\}\]