Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đà Nẵng năm học 2025-2026 có đáp án

a) \(A = \sqrt 4  + \sqrt 8  + \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}}  - 3\sqrt 2 \)

\( = 2 + \sqrt {4.2}  + \left| {1 - \sqrt 2 } \right| - 3\sqrt 2 \)

   \( = 2 + 2\sqrt 2  + \sqrt 2  - 1 - 3\sqrt 2 \)\( = 1\).

Vậy \(A = 1\).

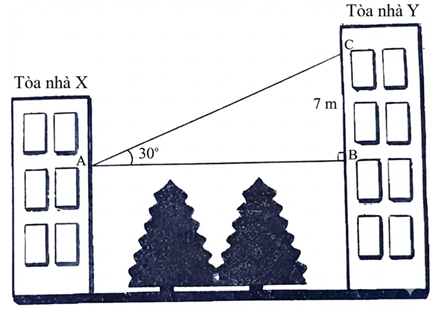
b) Xét tam giác ABC vuông tại B, ta có:

\({\rm{tan}}\,\widehat {BAC} = \frac{{BC}}{{AB}}\)  hay \({\rm{tan}}30^\circ  = \frac{7}{{AB}}\)  nên\(AB = \frac{7}{{{\rm{tan}}\,30^\circ }} = 7\sqrt 3  \approx 12,1\,\,({\rm{m}}).\)

Vậy khoảng cách AB giữa hai tòa nhà khoảng 12,1 mét.

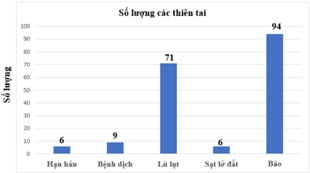
c) Biểu đồ có 5 loại thiên tai. Loại thiên tai xảy ra nhiều nhất là bão.

d) Bảng tấn số:

Ta có điều kiện xác định: \(x \ne  - 1;x \ne 1\).                                                                                

\(\frac{{x + 1}}{{x - 1}} + \frac{{x - 1}}{{x + 1}} = \frac{{3x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)                                                                                

\(\frac{{{{(x + 1)}^2} + {{(x - 1)}^2} - \left( {3x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = 0\)                                                                                

\(\frac{{{x^2} + 2x + 1 + {x^2} - 2x + 1 - 3x - 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = 0\)                                                                                

\(\frac{{2{x^2} - 3x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = 0\)                                                                                

Giải phương trình \(2{x^2} - 3x + 1 = 0\) ta được \(x = 1\) (loại) và \(x = \frac{1}{2}\left( {{\rm{tmdk}}} \right)\).                                                                                

Vậy phương trình \(\frac{{x + 1}}{{x - 1}} + \frac{{x - 1}}{{x + 1}} = \frac{{3x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\) có nghiệm \(x = \frac{1}{2}\).

Gọi giá vé niêm yết ban đầu của người lớn và trẻ em lần lượt là \(x,y\) (triệu đồng) \((x > 0;y > 0)\)

Giá vé người lớn được giảm \(20\% \), thực tế phải trả là \(80\% x = 0,8x\) (triệu đồng).

Giá vé trẻ em được giảm \(25\% \) nên thực tế phải trả là \(75\% y = 0,75y\) (triệu đồng)

Do giá vé ban đầu của 3 người lớn và 2 trẻ em là 4,2 triệu đồng nên: \(3x + 2y = 4,2\)

Giá vé sau giảm của 3 người lớn và 2 trẻ em là 3,3 triệu đồng nên: \(2,4x + 1,5y = 3,3\)

Từ đó có hệ phương trình:

   \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 4,2}\\{2,4x + 1,5y = 3,3}\end{array}} \right.\)

   \(\left\{ {\begin{array}{*{20}{l}}{x = \frac{{4,2 - 2y}}{3}}\\{2,4\left( {\frac{{4,2 - 2y}}{3}} \right) + 1,5y = 3,3}\end{array}} \right.\)

   \(\left\{ {\begin{array}{*{20}{l}}{x = \frac{{4,2 - 2y}}{3}}\\{3,36 - 0,1y = 3,3}\end{array}} \right.\)

   \(\left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 0,6}\end{array}} \right.\)

Vậy giá vé niêm yết của người lớn và trẻ em lần lượt là 1 triệu đồng và 600 nghìn đồng.

Ta có bằng giá trị sau:

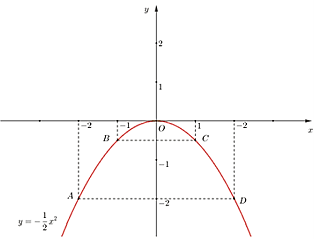
Đồ thị hàm số là đường cong parabol đi qua các điểm:

\(O\left( {0;0} \right);A\left( { - 2; - 2} \right);B\left( { - 1; - \frac{1}{2}} \right);C\left( {1; - \frac{1}{2}} \right);D\left( {2; - 2} \right)\)

Hệ số \(a =  - \frac{1}{2} < 0\) nên parabol có bề lõm hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số \(y =  - \frac{1}{2}{x^2}\) như sau:

Vì tung độ bằng 5 lần hoành độ nên ta có \(y = 5x\), thay vào hàm số \(y =  - \frac{1}{2}{x^2}\), ta được:

\(5x =  - \frac{1}{2}{x^2}\)

\({x^2} + 10x = 0\)

\(x\left( {x + 10} \right) = 0\)

Suy ra \(x = 0\) và \(x =  - 10\)

Với \(x = 0\) thì \(y = 0\)

Với \(x =  - 10\) thì \(y =  - 50\)

Vậy các điểm có toạ độ \(\left( {0;0} \right)\) và \(\left( { - 10; - 50} \right)\) thuộc đồ thị \(\left( P \right)\) có tung độ bằng 5 lần hoành độ.

Nửa chu vi bế bơi là \(36:2 = 18\left( {\rm{m}} \right)\)

   Gọi chiều dài của bể bơi lần lượt là \(x\left( {\rm{m}} \right)\,\,\left( {0 < x < 18} \right).\)

   Chiều rộng của bế bơi là \(18 - x\left( {\rm{m}} \right)\)

   Diện tích bế bơi là \(x\left( {18 - x} \right)\left( {{{\rm{m}}^2}} \right)\)

   Vì diện tích hình chữ nhật là \(80\,\,{{\rm{m}}^2}\) nên ta có phương trình \(x\left( {18 - x} \right) = 80\) \( - {x^2} + 18x - 80 = 0\)

\( - {x^2} + 18x - 80 = 0\)

\({x^2} - 18x + 80 = 0\)

\({x^2} - 10x - 8x + 80 = 0\)

\(x\left( {x - 10} \right) - 8\left( {x - 10} \right) = 0\)

\(\left( {x - 10} \right)\left( {x - 8} \right) = 0\)

\(x = 8\) hoặc \(x = 10\)

Vì chiều dài lớn hơn chiều rộng nên chiều dài bể bơi là 10 m, chiều rộng bể bơi là 8 m.

   Diện tích phần gạch lát là: \(12.10 - 80 = 40\left( {{{\rm{m}}^2}} \right)\)

Do BE, CF là các đường cao nên \(\Delta BFC\) vuông tại F suy ra B, F, C cùng thuộc đường tròn đường kính BC và \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\)cùng thuộc đường tròn đường kính BC

Vậy B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC là tứ giác nội tiếp

Khi đó \(\widehat {BCE} + \widehat {BFE} = 180^\circ \) (tổng hai góc đổi của từ giác nội tiếp)

Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kè bù) nên \(\widehat {AFE} = \widehat {ACB}\).

b) Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ  = 120^\circ \) (cùng chắn cung BC)

Khi đó \({S_q} = \frac{{\pi  \cdot {R^2} \cdot 120}}{{360}} = \frac{{\pi  \cdot {3^2} \cdot 120}}{{360}} \approx 9,42\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

c) Ta có \(\Delta OAB\) cân tại \(O\) nên:

\[\widehat {OAB} = \widehat {OBA} = \frac{{180^\circ  - \widehat {AOB}}}{2} = 90^\circ  - \frac{{\widehat {AOB}}}{2} = 90^\circ  - \widehat {ACB}.\]

Lại có BFEC nội tiếp nên \(\widehat {AEF} = \widehat {BCA}\) (cùng bù \(\widehat {BFE}\))

Suy ra \(\widehat {OAB} + \widehat {AFE} = 90^\circ  - \widehat {ACB} + \widehat {ACB} = 90^\circ \) hay \(\Delta AMF\) vuông tại M

Suy ra \(AO \bot EF\)

Mà \(AK \bot EF\) tại \(M\) nên \(A,K,M,O\) thẳng hàng

Xét \(\Delta AEF\) và \(\Delta ABC\) có

\(\widehat {BAC}\) chung

\(\widehat {AFE} = \widehat {ACB}\)

Do đó 

Mà \(K,\,\,H\) tương ứng là trực tâm của \(\Delta AEF,\,\,\Delta ABC\).

Và \(AM,\,\,AD\) tương ứng là các đường cao hạ từ \(A\) xuống \(EF,\,\,BC.\)

Do đó \(\frac{{AK}}{{AH}} = \frac{{AM}}{{AD}}\) hay \(\frac{{AK}}{{AM}} = \frac{{AH}}{{AD}}\)

Từ đó suy ra \(HK\,{\rm{//}}\,MD\) (theo định lí Thales đảo)