(1 điểm)

Trong một lần đi chơi Tết, hai bạn Diễm và Hằng được tặng mỗi người một phiếu quà tặng bằng cách bốc thăm ngẫu nhiên. Biết rằng, chi còn ba phiếu: một phiếu A trị giá 100 000 đồng, một phiếu B trị giá \[70\,\,000\] đồng và một phiếu C trị giá 50 000 đồng.

a) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?

b) Tính xác suất của biến cố “Tổng giá trị quà tặng của hai bạn ít hơn 160 000 đồng”.

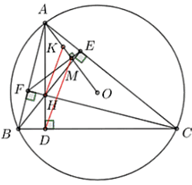
Do BE, CF là các đường cao nên \(\Delta BFC\) vuông tại F suy ra B, F, C cùng thuộc đường tròn đường kính BC và \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\)cùng thuộc đường tròn đường kính BC

Vậy B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC là tứ giác nội tiếp

Khi đó \(\widehat {BCE} + \widehat {BFE} = 180^\circ \) (tổng hai góc đổi của từ giác nội tiếp)

Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kè bù) nên \(\widehat {AFE} = \widehat {ACB}\).

b) Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ  = 120^\circ \) (cùng chắn cung BC)

Khi đó \({S_q} = \frac{{\pi  \cdot {R^2} \cdot 120}}{{360}} = \frac{{\pi  \cdot {3^2} \cdot 120}}{{360}} \approx 9,42\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

c) Ta có \(\Delta OAB\) cân tại \(O\) nên:

\[\widehat {OAB} = \widehat {OBA} = \frac{{180^\circ  - \widehat {AOB}}}{2} = 90^\circ  - \frac{{\widehat {AOB}}}{2} = 90^\circ  - \widehat {ACB}.\]

Lại có BFEC nội tiếp nên \(\widehat {AEF} = \widehat {BCA}\) (cùng bù \(\widehat {BFE}\))

Suy ra \(\widehat {OAB} + \widehat {AFE} = 90^\circ  - \widehat {ACB} + \widehat {ACB} = 90^\circ \) hay \(\Delta AMF\) vuông tại M

Suy ra \(AO \bot EF\)

Mà \(AK \bot EF\) tại \(M\) nên \(A,K,M,O\) thẳng hàng

Xét \(\Delta AEF\) và \(\Delta ABC\) có

\(\widehat {BAC}\) chung

\(\widehat {AFE} = \widehat {ACB}\)

Do đó 

Mà \(K,\,\,H\) tương ứng là trực tâm của \(\Delta AEF,\,\,\Delta ABC\).

Và \(AM,\,\,AD\) tương ứng là các đường cao hạ từ \(A\) xuống \(EF,\,\,BC.\)

Do đó \(\frac{{AK}}{{AH}} = \frac{{AM}}{{AD}}\) hay \(\frac{{AK}}{{AM}} = \frac{{AH}}{{AD}}\)

Từ đó suy ra \(HK\,{\rm{//}}\,MD\) (theo định lí Thales đảo)

Nửa chu vi bế bơi là \(36:2 = 18\left( {\rm{m}} \right)\)

   Gọi chiều dài của bể bơi lần lượt là \(x\left( {\rm{m}} \right)\,\,\left( {0 < x < 18} \right).\)

   Chiều rộng của bế bơi là \(18 - x\left( {\rm{m}} \right)\)

   Diện tích bế bơi là \(x\left( {18 - x} \right)\left( {{{\rm{m}}^2}} \right)\)

   Vì diện tích hình chữ nhật là \(80\,\,{{\rm{m}}^2}\) nên ta có phương trình \(x\left( {18 - x} \right) = 80\) \( - {x^2} + 18x - 80 = 0\)

\( - {x^2} + 18x - 80 = 0\)

\({x^2} - 18x + 80 = 0\)

\({x^2} - 10x - 8x + 80 = 0\)

\(x\left( {x - 10} \right) - 8\left( {x - 10} \right) = 0\)

\(\left( {x - 10} \right)\left( {x - 8} \right) = 0\)

\(x = 8\) hoặc \(x = 10\)

Vì chiều dài lớn hơn chiều rộng nên chiều dài bể bơi là 10 m, chiều rộng bể bơi là 8 m.

   Diện tích phần gạch lát là: \(12.10 - 80 = 40\left( {{{\rm{m}}^2}} \right)\)