Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = - \frac{1}{2}{x^2}\). Tìm các điểm thuộc đồ thị \(\left( P \right)\) có tung độ bằng 5 lần hoành độ.
Quảng cáo
Trả lời:
Ta có bằng giá trị sau:
|
\(x\) |
\[ - 2\] |
\[ - 1\] |
0 |
1 |
2 |
|
\(y = - \frac{1}{2}{x^2}\) |
\[ - 2\] |
\( - \frac{1}{2}\) |
0 |
\( - \frac{1}{2}\) |
\[ - 2\] |
Đồ thị hàm số là đường cong parabol đi qua các điểm:
\(O\left( {0;0} \right);A\left( { - 2; - 2} \right);B\left( { - 1; - \frac{1}{2}} \right);C\left( {1; - \frac{1}{2}} \right);D\left( {2; - 2} \right)\)
Hệ số \(a = - \frac{1}{2} < 0\) nên parabol có bề lõm hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = - \frac{1}{2}{x^2}\) như sau:
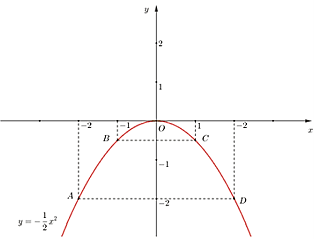
Vì tung độ bằng 5 lần hoành độ nên ta có \(y = 5x\), thay vào hàm số \(y = - \frac{1}{2}{x^2}\), ta được:
\(5x = - \frac{1}{2}{x^2}\)
\({x^2} + 10x = 0\)
\(x\left( {x + 10} \right) = 0\)
Suy ra \(x = 0\) và \(x = - 10\)
Với \(x = 0\) thì \(y = 0\)
Với \(x = - 10\) thì \(y = - 50\)
Vậy các điểm có toạ độ \(\left( {0;0} \right)\) và \(\left( { - 10; - 50} \right)\) thuộc đồ thị \(\left( P \right)\) có tung độ bằng 5 lần hoành độ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
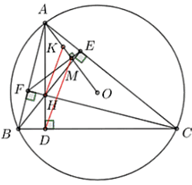
Do BE, CF là các đường cao nên \(\Delta BFC\) vuông tại F suy ra B, F, C cùng thuộc đường tròn đường kính BC và \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\)cùng thuộc đường tròn đường kính BC
Vậy B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC là tứ giác nội tiếp
Khi đó \(\widehat {BCE} + \widehat {BFE} = 180^\circ \) (tổng hai góc đổi của từ giác nội tiếp)
Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kè bù) nên \(\widehat {AFE} = \widehat {ACB}\).
b) Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ = 120^\circ \) (cùng chắn cung BC)
Khi đó \({S_q} = \frac{{\pi \cdot {R^2} \cdot 120}}{{360}} = \frac{{\pi \cdot {3^2} \cdot 120}}{{360}} \approx 9,42\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
c) Ta có \(\Delta OAB\) cân tại \(O\) nên:
\[\widehat {OAB} = \widehat {OBA} = \frac{{180^\circ - \widehat {AOB}}}{2} = 90^\circ - \frac{{\widehat {AOB}}}{2} = 90^\circ - \widehat {ACB}.\]
Lại có BFEC nội tiếp nên \(\widehat {AEF} = \widehat {BCA}\) (cùng bù \(\widehat {BFE}\))
Suy ra \(\widehat {OAB} + \widehat {AFE} = 90^\circ - \widehat {ACB} + \widehat {ACB} = 90^\circ \) hay \(\Delta AMF\) vuông tại M
Suy ra \(AO \bot EF\)
Mà \(AK \bot EF\) tại \(M\) nên \(A,K,M,O\) thẳng hàng
Xét \(\Delta AEF\) và \(\Delta ABC\) có
\(\widehat {BAC}\) chung
\(\widehat {AFE} = \widehat {ACB}\)
Do đó
Mà \(K,\,\,H\) tương ứng là trực tâm của \(\Delta AEF,\,\,\Delta ABC\).
Và \(AM,\,\,AD\) tương ứng là các đường cao hạ từ \(A\) xuống \(EF,\,\,BC.\)
Do đó \(\frac{{AK}}{{AH}} = \frac{{AM}}{{AD}}\) hay \(\frac{{AK}}{{AM}} = \frac{{AH}}{{AD}}\)
Từ đó suy ra \(HK\,{\rm{//}}\,MD\) (theo định lí Thales đảo)
Lời giải
Nửa chu vi bế bơi là \(36:2 = 18\left( {\rm{m}} \right)\)
Gọi chiều dài của bể bơi lần lượt là \(x\left( {\rm{m}} \right)\,\,\left( {0 < x < 18} \right).\)
Chiều rộng của bế bơi là \(18 - x\left( {\rm{m}} \right)\)
Diện tích bế bơi là \(x\left( {18 - x} \right)\left( {{{\rm{m}}^2}} \right)\)
Vì diện tích hình chữ nhật là \(80\,\,{{\rm{m}}^2}\) nên ta có phương trình \(x\left( {18 - x} \right) = 80\) \( - {x^2} + 18x - 80 = 0\)
\( - {x^2} + 18x - 80 = 0\)
\({x^2} - 18x + 80 = 0\)
\({x^2} - 10x - 8x + 80 = 0\)
\(x\left( {x - 10} \right) - 8\left( {x - 10} \right) = 0\)
\(\left( {x - 10} \right)\left( {x - 8} \right) = 0\)
\(x = 8\) hoặc \(x = 10\)
Vì chiều dài lớn hơn chiều rộng nên chiều dài bể bơi là 10 m, chiều rộng bể bơi là 8 m.
Diện tích phần gạch lát là: \(12.10 - 80 = 40\left( {{{\rm{m}}^2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

