Một gia đình dự dịnh xem Lễ hội Pháo hoa Quốc tế Đà Nẵng 2025 và vui chơi tại Khu Du Lịch S. Theo giá niêm yết, tổng giá vé vui chơi cho 3 người lớn và 2 trẻ em là 4,2 triệu đồng. Tuy nhiên, do mua vé đúng dịp khai mạc Lễ hội nên giá vé người lớn được giảm \(20\% \) và giá vé trẻ em được giảm \(25\% \) so với niêm yết. Vì vậy thực tế gia đình đó chì phải trả số tiền vé là 3,3 triệu đồng. Hỏi giá vé niêm yết của mỗi người lớn và mỗi trẻ em là bao nhiêu?

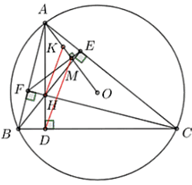
Do BE, CF là các đường cao nên \(\Delta BFC\) vuông tại F suy ra B, F, C cùng thuộc đường tròn đường kính BC và \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\)cùng thuộc đường tròn đường kính BC

Vậy B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC là tứ giác nội tiếp

Khi đó \(\widehat {BCE} + \widehat {BFE} = 180^\circ \) (tổng hai góc đổi của từ giác nội tiếp)

Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kè bù) nên \(\widehat {AFE} = \widehat {ACB}\).

b) Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ  = 120^\circ \) (cùng chắn cung BC)

Khi đó \({S_q} = \frac{{\pi  \cdot {R^2} \cdot 120}}{{360}} = \frac{{\pi  \cdot {3^2} \cdot 120}}{{360}} \approx 9,42\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

c) Ta có \(\Delta OAB\) cân tại \(O\) nên:

\[\widehat {OAB} = \widehat {OBA} = \frac{{180^\circ  - \widehat {AOB}}}{2} = 90^\circ  - \frac{{\widehat {AOB}}}{2} = 90^\circ  - \widehat {ACB}.\]

Lại có BFEC nội tiếp nên \(\widehat {AEF} = \widehat {BCA}\) (cùng bù \(\widehat {BFE}\))

Suy ra \(\widehat {OAB} + \widehat {AFE} = 90^\circ  - \widehat {ACB} + \widehat {ACB} = 90^\circ \) hay \(\Delta AMF\) vuông tại M

Suy ra \(AO \bot EF\)

Mà \(AK \bot EF\) tại \(M\) nên \(A,K,M,O\) thẳng hàng

Xét \(\Delta AEF\) và \(\Delta ABC\) có

\(\widehat {BAC}\) chung

\(\widehat {AFE} = \widehat {ACB}\)

Do đó 

Mà \(K,\,\,H\) tương ứng là trực tâm của \(\Delta AEF,\,\,\Delta ABC\).

Và \(AM,\,\,AD\) tương ứng là các đường cao hạ từ \(A\) xuống \(EF,\,\,BC.\)

Do đó \(\frac{{AK}}{{AH}} = \frac{{AM}}{{AD}}\) hay \(\frac{{AK}}{{AM}} = \frac{{AH}}{{AD}}\)

Từ đó suy ra \(HK\,{\rm{//}}\,MD\) (theo định lí Thales đảo)

Nửa chu vi bế bơi là \(36:2 = 18\left( {\rm{m}} \right)\)

   Gọi chiều dài của bể bơi lần lượt là \(x\left( {\rm{m}} \right)\,\,\left( {0 < x < 18} \right).\)

   Chiều rộng của bế bơi là \(18 - x\left( {\rm{m}} \right)\)

   Diện tích bế bơi là \(x\left( {18 - x} \right)\left( {{{\rm{m}}^2}} \right)\)

   Vì diện tích hình chữ nhật là \(80\,\,{{\rm{m}}^2}\) nên ta có phương trình \(x\left( {18 - x} \right) = 80\) \( - {x^2} + 18x - 80 = 0\)

\( - {x^2} + 18x - 80 = 0\)

\({x^2} - 18x + 80 = 0\)

\({x^2} - 10x - 8x + 80 = 0\)

\(x\left( {x - 10} \right) - 8\left( {x - 10} \right) = 0\)

\(\left( {x - 10} \right)\left( {x - 8} \right) = 0\)

\(x = 8\) hoặc \(x = 10\)

Vì chiều dài lớn hơn chiều rộng nên chiều dài bể bơi là 10 m, chiều rộng bể bơi là 8 m.

   Diện tích phần gạch lát là: \(12.10 - 80 = 40\left( {{{\rm{m}}^2}} \right)\)