Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2022-2023 sở GD&ĐT Quảng Bình có đáp án
47 người thi tuần này 4.6 93 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a)Với \(0 \le x \ne 1\) ta có:
\(\begin{array}{l}P = \frac{{\left( {3x + 5\sqrt x - 11} \right) - \left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right) + 2\left( {\sqrt x - 1} \right) - \left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\\ = \frac{{\left( {3x + 5\sqrt x - 11} \right) - \left( {x - 4} \right) + 2\left( {\sqrt x - 1} \right) - \left( {x + \sqrt x - 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\end{array}\)
\( = \frac{{x + 6\sqrt x - 7}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 7} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x + 7}}{{\sqrt x + 2}}\)
Vậy \(P = \frac{{\sqrt x + 7}}{{\sqrt x + 2}}\) với \(0 \le x \ne 1\)
b)Ta có: \(P = \frac{{\sqrt x + 7}}{{\sqrt x + 2}} = 1 + \frac{5}{{\sqrt x + 2}} \Rightarrow 1 < P \le 1 + \frac{5}{2} = \frac{7}{2}\) với \(0 \le x \ne 1\)
Biểu thức \[P\] chia hết cho 3\( \Leftrightarrow P = 3 \Leftrightarrow \frac{{\sqrt x + 7}}{{\sqrt x + 2}} = 3\)
\( \Leftrightarrow \sqrt x + 7 = 3\sqrt x + 6 \Leftrightarrow \sqrt x = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}\)
Vậy \(x = \frac{1}{4}\)
Lời giải
a)Ta thấy \(ac = - 3 < 0,{\rm{ }}\forall m\) nên phương trình (1) luôn có 2 nghiệm \[{x_1},{\rm{ }}{x_2}\] với mọi giá trị của \(m\).
Theo hệ thức Vi-ét ta có: \[\left\{ \begin{array}{l}{x_1} + {\rm{ }}{x_2} = 2m - 2{\rm{ }}\left( 2 \right)\\{x_1}{x_2} = - 3{\rm{ }}\left( 3 \right)\end{array} \right.\]
Kết hợp \[{x_1} + 2{x_2} = 5\] với \(\left( 2 \right)\) ta được \[{x_1} = 4m - 9,{\rm{ }}{x_2} = 7 - 2m\]
Thay vào \(\left( 3 \right)\) ta có
\[\left( {4m - 9} \right)\left( {7 - 2m} \right) = - 3 \Leftrightarrow - 8{m^2} + 46m - 60 = 0 \Leftrightarrow m = 2\] hoặc \[m = \frac{{15}}{4}\]
Vậy \[m = 2\]
b)Điều kiện: \(x \ge \frac{5}{3}\)
\(\begin{array}{l}\sqrt {x + 1} + \sqrt {3x - 5} = 4 \Leftrightarrow \left( {\sqrt {x + 1} - 2} \right) + \left( {\sqrt {3x - 5} - 2} \right) = 0\\ \Leftrightarrow \frac{{x - 3}}{{\sqrt {x + 1} + 2}} + \frac{{3\left( {x - 3} \right)}}{{\sqrt {3x - 5} + 2}} = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 3} \right)\left[ {\frac{1}{{\sqrt {x + 1} + 2}} + \frac{3}{{\sqrt {3x - 5} + 2}}} \right] = 0\\ \Leftrightarrow x - 3 = 0{\rm{ do }}\frac{1}{{\sqrt {x + 1} + 2}} + \frac{3}{{\sqrt {3x - 5} + 2}} > 0,{\rm{ }}\forall x \ge \frac{5}{3}\\ \Leftrightarrow x = 3\end{array}\)
Vậy \[x = 3\]
Lời giải
Đặt \(\left\{ {\begin{array}{*{20}{c}}{x = a + b - c > 0}\\{y = b + c - a > 0}\\{z = c + a - b > 0}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{{x + z}}{2}}\\{b = \frac{{x + y}}{2}}\\{c = \frac{{y + z}}{2}}\end{array}} \right.\)
Ta cần chứng minh: \(\frac{{{{\left( {x + y} \right)}^2}}}{{4z}} + \frac{{{{\left( {y + z} \right)}^2}}}{{4x}} + \frac{{{{\left( {z + x} \right)}^2}}}{{4y}} \ge x + y + z\)
Ta có: \(\frac{{{{\left( {x + y} \right)}^2}}}{{4z}} + \frac{{{{\left( {y + z} \right)}^2}}}{{4x}} + \frac{{{{\left( {z + x} \right)}^2}}}{{4y}} \ge \frac{{xy}}{z} + \frac{{yz}}{x} + \frac{{zx}}{y}{\rm{ }}\left( 1 \right)\)
Mặt khác: \(\frac{{xy}}{z} + \frac{{yz}}{x} \ge 2y;{\rm{ }}\frac{{yz}}{x} + \frac{{zx}}{y} \ge 2z;{\rm{ }}\frac{{xy}}{z} + \frac{{zx}}{y} \ge 2x\).
Khi đó \(\frac{{xy}}{z} + \frac{{yz}}{x} + \frac{{zx}}{y} \ge x + y + z{\rm{ }}\left( 2 \right)\)
Từ \(\left( 1 \right){\rm{, }}\left( 2 \right)\) ta có \(\frac{{{{\left( {x + y} \right)}^2}}}{{4z}} + \frac{{{{\left( {y + z} \right)}^2}}}{{4x}} + \frac{{{{\left( {z + x} \right)}^2}}}{{4y}} \ge x + y + z\)
Vậy \(\frac{{{a^2}}}{{b + c - a}} + \frac{{{b^2}}}{{c + a - b}} + \frac{{{c^2}}}{{a + b - c}} \ge a + b + c\)
Dấu bằng xãy ra khi \[a = b = c\]
Lời giải
Với \(n \in \mathbb{N}\), ta có \({n^5} + 1 \vdots {n^3} + 1 \Leftrightarrow {n^2}\left( {{n^3} + 1} \right) - \left( {{n^2} - 1} \right) \vdots {n^3} + 1\)
\( \Leftrightarrow \left( {{n^2} - 1} \right) \vdots {n^3} + 1 \Leftrightarrow \left( {n - 1} \right)\left( {n + 1} \right) \vdots \left( {n + 1} \right)\left( {{n^2} - n + 1} \right)\)
\( \Leftrightarrow n - 1 \vdots {n^2} - n + 1\) (vì \(n + 1 \ne 0\))
\( \Rightarrow n\left( {n - 1} \right) \vdots {n^2} - n + 1 \Leftrightarrow \left( {{n^2} - n + 1} \right) - 1 \vdots {n^2} - n + 1\)
\( \Leftrightarrow 1 \vdots {n^2} - n + 1 \Rightarrow \left[ \begin{array}{l}{n^2} - n + 1 = 1\\{n^2} - n + 1 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}n = 1\\n = 0\end{array} \right.\)
Thử lại ta thấy \(n = 0;\,{\rm{ }}n = 1\) thỏa mãn để \({n^5} + 1\) chia hết cho \({n^3} + 1\)
Vậy \(n = 0;\,{\rm{ }}n = 1.\)
Lời giải
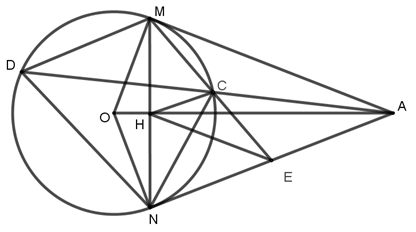
a)Ta có \(AM,{\rm{ }}AN\) là hai tiếp tuyến cắt nhau nên \(OA\) là đường phân giác của \(\widehat {MON}\)
\(\Delta MON\) cân tại \(O\), có \(OA\)đường phân giác nên \(OA\)đồng thời cũng là đường trung trực ứng với \(MN\)\( \Rightarrow MH = HN;{\rm{ }}OA \bot MN\)
Vì \(MH = HN;{\rm{ }}AE = EN\) nên \(HE\) là đường trung bình của \(\Delta MAN\)
\( \Rightarrow HE//MA \Rightarrow \widehat {HEM} = \widehat {AME}\)
mà \(\widehat {MNC} = \widehat {AME}\) (cùng chắn )
nên \(\widehat {MNC} = \widehat {HEM}\)
Suy ra tứ giác \(HCEN\) nội tiếp.
b)mà \(EN = EA\) nên \[\frac{{EA}}{{EM}} = \frac{{EC}}{{EA}}\,\,\]
\[\Delta ECA\,\]và \[\Delta EAM\] có \[\frac{{EA}}{{EM}} = \frac{{EC}}{{EA}}\,\,\]và \(\widehat {AEC}\) chung
Do đó \( \Rightarrow \widehat {EAC} = \widehat {EMA}\)
Lại có \(\widehat {EMA} = \widehat {MDC}\) (cùng chắn ) nên \(\widehat {EAC} = \widehat {MDC}\)
Suy ra \(MD//AN\)\( \Rightarrow \widehat {DMN} = \widehat {MNA}\)
Mặt khác, \(\widehat {MDN} = \widehat {MNA}\)(cùng chắn )
\( \Rightarrow \widehat {MDN} = \widehat {DMN}\). Do đó \[\Delta MND\,\]cân tại N
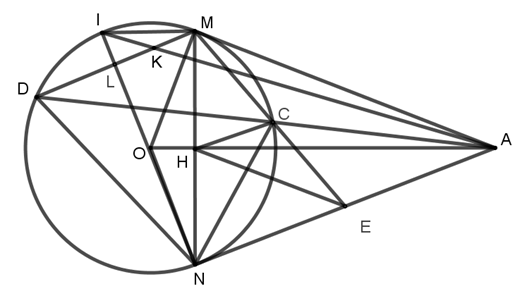
Gọi \(L\)là giao điểm của \(MD\) và \(NI\)
Vì \(MD//AN\)(cmt), \(IN \bot AN\) (tính chất tiếp tuyến)
nên \(IN \bot MD\) tại \(L\)\( \Rightarrow DL = ML = \frac{{MD}}{2}\)
\[\Delta INA\,\]có \(LK//AN\)\[ \Rightarrow \frac{{LK}}{{AN}} = \frac{{IL}}{{IN}}\,\,{\rm{ }}\left( 1 \right)\]
Ta có \(IM//AO\) (cùng vuông góc với \(MN\)), suy ra \(\widehat {MIL} = \widehat {AON}\)
Lại có \(\widehat {MLI} = \widehat {ONA} = {90^0}\) nên
Suy ra \[\frac{{IL}}{{NO}} = \frac{{ML}}{{AN}}\,\, \Rightarrow \frac{{IL}}{{2NO}} = \frac{{ML}}{{2AN}} \Rightarrow \frac{{IL}}{{IN}} = \frac{{ML}}{{2AN}}\,{\rm{ }}\,\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[\frac{{LK}}{{AN}} = \frac{{ML}}{{2AN}}\,\, \Rightarrow LK = \frac{{ML}}{2} \Rightarrow MK = KL = \frac{{ML}}{2}\]
Vì \[MK = LK;{\rm{ }}ML = DL \Rightarrow KD = 3KM \Rightarrow \frac{{KM}}{{KD}} = \frac{1}{3}.\]