Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 38
64 người thi tuần này 4.6 117 lượt thi 9 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
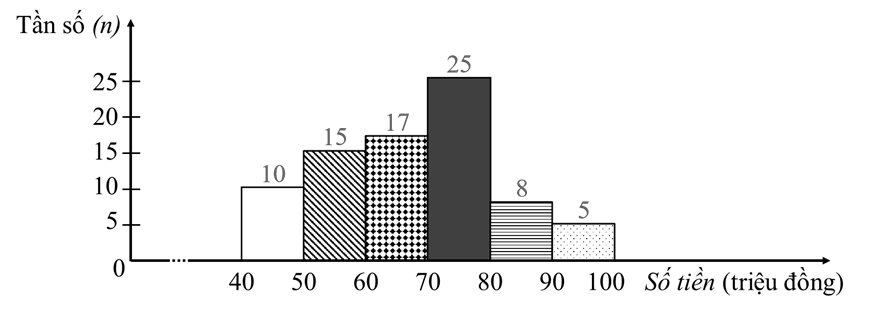
Đoạn văn 1
Lời giải
|
Nhóm |
Tần số tương đối (%) |
|
\[\left[ {40\,;\,50} \right)\] |
\[12,5\] |
|
\[\left[ {5\,0\,;\,60} \right)\] |
\[18,75\] |
|
\[\left[ {60\,;\,70} \right)\] |
\[21,25\] |
|
\[\left[ {70\,;\,80} \right)\] |
\[31,25\] |
|
\[\left[ {80\,;\,90} \right)\] |
\[10\] |
|
\[\left[ {90\,;\,100} \right)\] |
\[6,25\] |
|
Cộng |
\[100\] |
Lời giải
Không gian mẫu là: \[\Omega = \left\{ {\left\{ {1;2} \right\};\left\{ {1;3} \right\};\left\{ {1;4} \right\};\left\{ {1;5} \right\};\left\{ {2;3} \right\};\left\{ {2;4} \right\};\left\{ {2;5} \right\};\left\{ {3;4} \right\};\left\{ {3;5} \right\};\left\{ {4;5} \right\}} \right\}.\]
Do đó, tập hợp \[\Omega \] có \[10\] phần tử.
Do các viên bi có kích thước, khối lượng như nhau và được lấy ngẫu nhiên nên các kết quả trên là đồng khả năng.
Gọi \[A\] là biến cố: “Hai viên bi được lấy ra khác màu”.
Có \[6\] khả năng thuận lợi của biến cố \[A\] là \[\left\{ {1;4} \right\};\left\{ {1;5} \right\};\left\{ {2;4} \right\};\left\{ {2;5} \right\};\left\{ {3;4} \right\};\left\{ {3;5} \right\}.\]
Vậy \[P\left( A \right) = \frac{6}{{10}} = \frac{3}{5}\].
Lời giải
1) Với \(x = 9\) (TMĐK) thay vào biểu thức \(Q\) ta được: \(Q = \frac{1}{{3 + 2}} = \frac{1}{5}\)
Vậy \(x = 9\) thì biểu thức \(Q = \frac{1}{5}\).
2) Với \(x \ge 0;x \ne 4\) ta có:
\(P = \frac{{3\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{8\sqrt x }}{{x - 4}}\)
\( = \frac{{3\sqrt x (\sqrt x - 2) - \sqrt x (\sqrt x + 2) + 8\sqrt x }}{{(\sqrt x - 2)(\sqrt x + 2)}}\)
\( = \frac{{3x - 6\sqrt x - x - 2\sqrt x + 8\sqrt x }}{{(\sqrt x - 2)(\sqrt x + 2)}}\)
\( = \frac{{2x}}{{(\sqrt x - 2)(\sqrt x + 2)}}\)
3) Với \(x \ge 0;x \ne 4\) ta có: \(M = \frac{P}{Q} = \frac{{2x}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}:\frac{1}{{\sqrt x + 2}} = \frac{{2x}}{{\sqrt x - 2}}\)
Để \(M = 18\) thì \(\frac{{2x}}{{\sqrt x - 2}} = 18\)
\(x - 9\sqrt x + 18 = 0\)
\(\left( {\sqrt x - 3} \right)\left( {\sqrt x - 6} \right) = 0\)
\(\sqrt x = 3\) hoặc \(\sqrt x = 6\)
\(x = 9\) hoặc \(x = 36\) (thoả mãn điều kiện)
Vậy để \(M = 18\) thì \(x \in \left\{ {9;36} \right\}\).
Lời giải
Gọi số lần giảm giá \[100{\rm{ 000}}\]đồng/1tour để thu được doanh thu lớn nhất là \[x\] (lần)
Sau \[x\] lần giảm thì giá của một tour là: \[2{\rm{ }}000{\rm{ }}000 - 100{\rm{ }}000.x\] (đồng).
Vì cứ sau \[1\] lần giảm thì có thêm \[20\] người tham gia nên sau \[x\] lần giảm thì có thêm \[20.x\](người tham gia) nên tổng số người tham gia sau \[x\] lần giảm giá là: \[200 + 20.x\] (người )
Tổng doanh thu sau \[x\] lần giảm giá là:
\[S = \left( {2{\rm{ }}000{\rm{ }}000 - 100{\rm{ }}000.x} \right).\left( {200 + 20.x} \right)\](đồng)
\[S = 100{\rm{ }}000.20.\left( {20 - x} \right).\left( {10 + x} \right)\](đồng)
\[S = 2{\rm{ 0}}00{\rm{ }}000.\left( { - {x^2} + 10x + 200} \right)\] (đồng)
Xét \[ - {x^2} + 10{\rm{x + 200 = }} - {\rm{(}}{{\rm{x}}^2} - 10{\rm{x + 25}} - 25 - 200)\] \[ = - {{\rm{(x}} - 5)^2} + 225\]
Vì \[ - {{\rm{(x}} - 5)^2} + 225 \le 225\] nên \[2{\rm{ 0}}00{\rm{ }}000.\left( { - {x^2} + 10x + 200} \right) \le 2\,\,000\,\,000.225 = 450\,\,000\,\,000\]
hay\[S \le 450\,\,000\,\,000\]
\[{S_{m{\rm{ax}}}} = 450\,\,000\,\,000\]
Khi đó x = 5 (lần)
Vậy giá tour khi đó: \[2{\rm{ }}000{\rm{ }}000 - 100{\rm{ }}000.5 = 1{\rm{ 500 000}}\] (đồng).
Đoạn văn 2
Lời giải
Gọi \(x\) và \(y\) lần lượt là số mililít dung dịch HCl nồng độ \(8\% \) và \(20\% \) cần sử dụng để tạo thành \(36\) ml dung dịch HCl nồng độ \(12\% \). Điều kiện: \(x > 0,y > 0\)
Vì Bình muốn pha \(36\) ml dung dịch HCl nồng độ \(12\% \) nên ta có phương trình: \(x + y = 36\)
Mặt khác, Bình muốn pha \(36\) ml dung dịch HCl có nồng độ \(12\% \) từ các dung dịch \({\rm{HCl}}\,\,\,\,8\% \) và \(20\% \) nên ta có phương trình: \(8\% x + 20\% y = 12\% \cdot 36\) hay \(0,08x + 0,2y = 4,32\)
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\,\,\,\,\,\,\,\,\,\,x + \,\,\,\,\,\,\,\,\,y = 36\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)}\\{0,08x + 0,2y = 4,32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\)
Nhân hai vế của phương trình \(\left( 1 \right)\) với \(0,08\) ta được: \(\left\{ {\begin{array}{*{20}{l}}{0,08x + 0,08y = 2,88\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)}\\{0,08x + \,\,\,0,2y = 4,32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)}\end{array}} \right.\)
Trừ từng vế hai phương trình \(\left( 3 \right)\)và \(\left( 4 \right)\)ta được \(0,12y = 1,44\) hay \(y = 12\).
Thay \(y = 12\) vào phương trình \(\left( 1 \right)\) ta được \(x = 24\).
Các giá trị tìm được này thoả mãn các điều kiện của ẩn.
Vậy bạn Bình cần sử dụng khoảng \(24\) ml dung dịch HCl nồng độ \(8\% \) và \(12\) ml dung dịch HCl nồng độ \(20\% \) để pha chế \(36\) ml dung dịch HCl nồng độ \(12\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.