Đề thi tuyển sinh vào lớp 10 Toán năm học 2015 - 2016 Sở GD&ĐT Hà Nội có đáp án

Giải hệ phương trình \[\left\{ \begin{array}{l}2\left( {x + y} \right) + \sqrt {x + 1}  = 4\\\left( {x + y} \right) - 3\sqrt {x + 1}  =  - 5\end{array} \right.\]

Điều kiện: \(x \ge  - 1\).

Đặt \(\left\{ \begin{array}{l}x + y = a\\\sqrt {x + 1}  = b\end{array} \right.\)

Khi đó hệ phương trình trở thành:

\[\left\{ \begin{array}{l}2a + b = 4\\a - 3b =  - 5\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}2a + b = 4\\2a - 6b =  - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a + b = 4\\7b = 14\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}2a = 4 - b\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a = 2\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\end{array} \right.\]

Khi đó \(\left\{ \begin{array}{l}x + y = 1\\\sqrt {x + 1}  = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1 - x\\x + 1 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y =  - 2\\x = 3\end{array} \right.\) (thỏa mãn điều kiện)

Kết luận: Hệ phương trình có nghiệm là \(\left( {3; - 2} \right)\).

1)

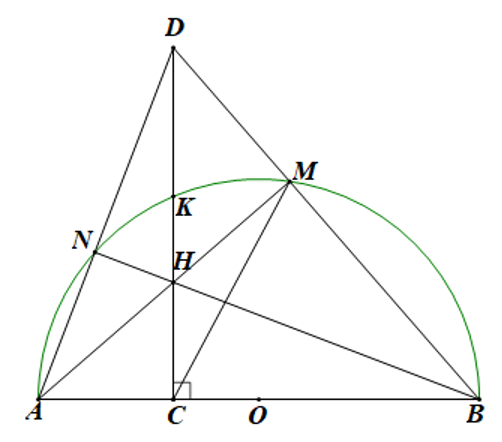
Chứng minh tứ giác \[ACMD\] là tứ giác nội tiếp.

0,25

Vì \(M\) nằm trên nửa đường tròn tâm \(O\), đường kính \(AB\) nên \(\widehat {AMB} = 90^\circ  \Rightarrow \widehat {AMD} = 90^\circ \)

0,25

Vì \(DC \bot AB\) nên \(\widehat {ACD} = 90^\circ \).

Do đó \(\widehat {AMD} = \widehat {ACD} = 90^\circ \) nên \(M,C\) thuộc đường tròn đường kính \(AD\)

0,25

Kết luận: \(ACMD\) là tứ giác nội tiếp.

0,25

2)

Chứng minh \[CA.CB = CH.CD\].

1,0

Xét \(\Delta CAH\) và \(\Delta CDB\) có:

\(\widehat {ACH} = \widehat {DCB} = 90^\circ \);

0,25

\(\widehat {CAH} = \widehat {CDB}\) (cùng phụ với \(\widehat {CBM}\))

0,25

Do đó

0,25

Suy ra \(\frac{{CA}}{{CD}} = \frac{{CH}}{{CB}}\) (tỉ số đồng dạng)

Nên \(CA.CB = CH.CD\) (điều phải chứng minh).

0,25

3)

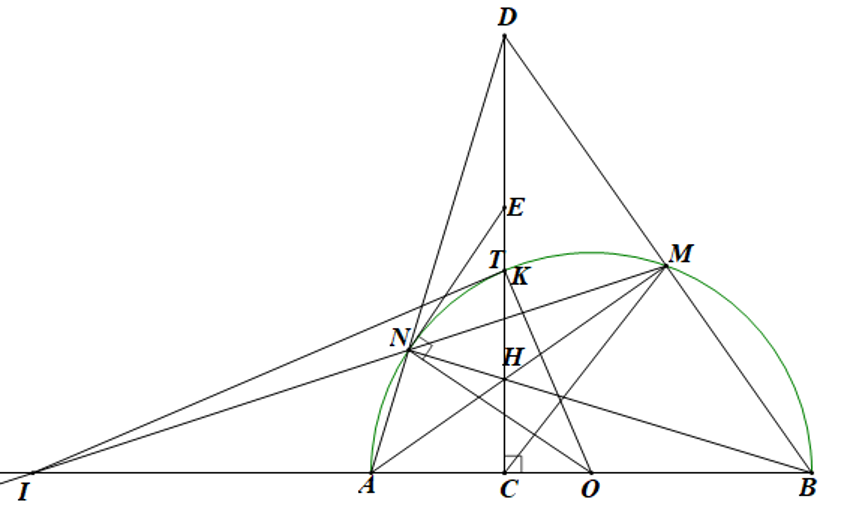
Chứng minh ba điểm \(A,N,D\) thẳng hàng và tiếp tuyến tại \(N\) của nửa đường tròn đi qua trung điểm của \[DH\].

1,0

Xét \(\Delta ABD\) có \(AM \bot BD,DC \bot AB\) và \(AM,DC\) cắt nhau tại \(H\)

Nên \(H\) là trực tâm của \(\Delta ABD\)

\( \Rightarrow BH \bot AD\) hay \(BN \bot AD\)

0,25

Vì \(N\) nằm trên nửa đường tròn tâm \(O\), đường kính \(AB\) nên \(\widehat {ANB} = 90^\circ  \Rightarrow AN \bot BN\)

Vì \(BN \bot AD\) và \(AN \bot BN\) nên ba điểm \(A,N,D\) thẳng hàng.

0,25

Gọi \(E\) là giao điểm của \(CK\) và tiếp tuyến tại \(N\)

Ta có \(BN \bot DN\) nên \(\widehat {BNO} + \widehat {BNE} = 90^\circ \)

Vì \(ON \bot EN\) nên \(\widehat {BNE} + \widehat {DNE} = 90^\circ \)

Suy ra \[\widehat {BNO} = \widehat {DNE}\]

Mà \(\widehat {BNO} = \widehat {OBN},\widehat {OBN} = \widehat {EDN}\) nên \(\widehat {DNE} = \widehat {EDN}\)

\( \Rightarrow \Delta DEN\) cân tại \(E\)

\( \Rightarrow ED = EN\)        \(\left( 1 \right)\)

0,25

Ta có: \(\widehat {ENH} = 90^\circ  - \widehat {END} = 90^\circ  - \widehat {NDH} = \widehat {EHN}\)

\( \Rightarrow \Delta HEN\) cân tại \(E\)

\( \Rightarrow EH = EN\)        \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(E\) là trung điểm của \(HD\) (điều phải chứng minh).

0,25

4)

Khi \(M\) di động trên cung \[KB\], chứng minh đường thẳng \[MN\] luôn đi qua một điểm cố định.

0,5

Gọi \(I\) là giao điểm của \[MN\] và \(AB\).

Kẻ tia \(IT\) là tiếp tuyến của nửa đường tròn với \(T\) là tiếp điểm

\( \Rightarrow IN.IM = I{T^2}\)         \(\left( 3 \right)\)

Ta có \[EM \bot OM\] (vì \(\Delta ENO = \Delta EMO\) và \(EN \bot ON\))

\( \Rightarrow N,C,O,M\) cùng thuộc một đường tròn

\( \Rightarrow IN.IM = IC.IO\)      \(\left( 4 \right)\)

0,25

Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra

\( \Rightarrow CT \bot IO\) \( \Rightarrow T \equiv K\)

\( \Rightarrow I\) là giao điểm của tiếp tuyến tại \(K\) của nửa đường tròn và đường thẳng \(AB\)

\( \Rightarrow I\) cố định

\( \Rightarrow \)Đường thẳng \(MN\) luôn đi qua điểm \(I\) cố định (điều phải chứng minh).

0,25