Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Quảng Bình có đáp án

Ta có \(2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\) \( \Leftrightarrow 2\left( {m - 3} \right) + 3 = 2\)

\( \Leftrightarrow m = \frac{5}{2}\left( {TM} \right)\). Vậy \(m = \frac{5}{2}\).

Ta có \(P = {\left( {3x} \right)^2} - 2.2.3x + {2^2} - 2\left| {3x - 2} \right| + 2024\)

             \( = {\left( {3x - 2} \right)^2} - 2\left| {3x - 2} \right| + 1 + 2023\)

             \( = {\left( {\left| {3x - 2} \right| - 1} \right)^2} + 2023 \ge 2023,\forall x \in \mathbb{R}\)

Dấu bằng xảy ra khi và chỉ khi

\(\left| {3x - 2} \right| - 1 = 0 \Leftrightarrow \left| {3x - 2} \right| = 1\)                                                       \( \Leftrightarrow \left[ \begin{array}{l}3x - 2 = 1\\3x - 2 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{1}{3}\end{array} \right.\)

Vậy giá trị nhỏ nhất của \(P\) là 2023 đạt được khi \(x = 1\) hoặc \(x = \frac{1}{3}\).

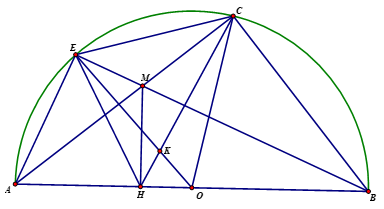
1.Xét tứ giác BCMH có

\(\widehat {BCM} = \widehat {ACB} = {90^0}\)(góc nội tiếp chắn nửa đường tròn)

\(\widehat {MHB} = {90^0}\) (vì \(MH \bot AB\))

Suy ra \(\widehat {BCM} + \widehat {MHB} = {180^0}\)nên tứ giác BCMH nội tiếp đường tròn.

2.Xét \(\Delta ACE\) và \(\Delta HCM\) có: \(\widehat {EAC} = \widehat {EBC}\)(Cùng chắn cung )

\(\widehat {MHC} = \widehat {EBC}\)(Cùng chắn cung )

Suy ra \(\widehat {EAC} = \widehat {MHC}{\rm{  }}\left( 1 \right)\)

Tương tự ta có \(\widehat {ACE} = \widehat {MCH}{\rm{  }}\left( 2 \right)\), (cùng bằng \(\widehat {ABE}\))

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\Delta ACE\) ∽ \(\Delta HCM{\rm{  }}\left( {g - g} \right)\) (đpcm)

3.Chứng minh được tứ giác AEMH nội tiếp

Suy ra \(\widehat {CAB} = \widehat {MEH}\) (Cùng chắn cung )    

Mà \(\widehat {CAB} = \widehat {CEB}\) (Cùng chắn cung )    

Suy ra \(\widehat {CAB} = \widehat {MEH} = \widehat {CEB}\)

Ta có \(\widehat {COB} = 2.\widehat {CAB}\) (góc nội tiếp và góc ở tâm cùng chắn )

Do đó \(\widehat {COB} = 2.\widehat {CEB} = \widehat {CEH}\) nên tứ giác CEHO nội tiếp

Suy ra \(\widehat {HEO} = \widehat {HCO}\) và \(\widehat {EHC} = \widehat {EOC}\)

Nên \(\Delta EKH\) ∽ \(\Delta CKO{\rm{  }}\left( {g - g} \right)\)

\( \Rightarrow \frac{{KE}}{{KC}} = \frac{{KH}}{{KO}}\)\( \Rightarrow KE.KO = KC.KH\)