Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Sư Phạm Hà Nội có đáp án
41 người thi tuần này 4.6 83 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) A \( = \) \(\frac{{{x^2} + 8\sqrt x }}{{x - 2\sqrt x + 4}} + \frac{{2x + \sqrt x }}{{\sqrt x }} + \frac{{16 - 4x}}{{\sqrt x + 2}} = \frac{{\sqrt x .\left( {\sqrt {{x^3}} + 8} \right)}}{{x - 2\sqrt x + 4}} + \) \(2\sqrt x + 1 + 4\left( {2 - \sqrt x {\rm{\;}}} \right)\)
\( = {\rm{\;}}\sqrt x .\left( {\sqrt x + 2} \right) + 2\sqrt x + 1 + 4\left( {2 - \sqrt x {\rm{\;}}} \right) = x + 9\)
Vậy A \( = x + 9\)
b) Sau 1 giờ nhiệt độ của khay nước là \({125^{\rm{o}}}.80\% = {100^{\rm{o}}}\).
Sau 2 giờ nhiệt độ của khay nước là \({100^{\rm{o}}}.80\% = {80^{\rm{o}}}\).
Sau 3 giờ nhiệt độ của khay nước là \({80^{\rm{o}}}.80\% = {64^{\rm{o}}}\).
Dễ thấy nếu hơn 3 giờ thì nhiệt độ khay nước sẽ giảm xuống thấp hơn \({64^{\rm{o}}}{\rm{F}}\).
Vậy số giờ cần tìm là 3 giờ.
Lời giải
Các hệ số \(a = 1,b = - (2m + 1),c = - ({m^2} + 1)\)
Vì \(ac = - ({m^2} + 1) < 0\) nên phương trình (1) luôn có 2 nghiệm.
Hệ thức liên hệ không phụ thuộc vào m cần tìm là:\({x_1}.{x_2} + \frac{{{{({x_1} + {x_2} + 1)}^2}}}{4} + 1 = 0\)
b) Vì (P) \(y = a{x^2}\) đi qua điểm \(M( - 1,\frac{1}{2})\) nên \(a = \frac{1}{2}\)
Gọi toạ độ của M là \(({x_0},{y_0}) \Rightarrow {y_0} = \frac{1}{2}.{x_0}^2\)
Theo giả thiết đề bài ta suy ra:\(\left| {{x_0}} \right| = 2.\left| {{y_0}} \right| \Rightarrow \left| {{x_0}} \right| = {x_0}^2 \Rightarrow {x_0} \in \left\{ {0; \pm 1} \right\}\)
Do đó toạ độ điểm M cần tìm là \((0,0);(1,\frac{1}{2});( - 1,\frac{1}{2})\).
Lời giải
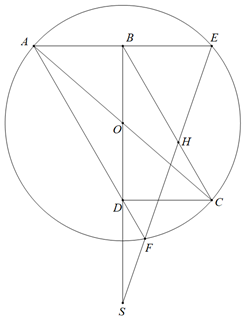
a) Đặt \(AB = a,BC = 2a\).Vì \(\widehat {ABC} = {120^0}\)\( \Rightarrow \)\(\widehat {BAD} = {60^0}\).
Áp dụng định lí cosin vào \(\Delta ABD\)ta có:
\(\begin{array}{l}B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\\ = {a^2} + 4{a^2} - 2.2a.a.\cos 60\\ = 5{a^2} - 2{a^2} = 3{a^2} \Rightarrow B{D^2} + A{B^2} = A{D^2}\end{array}\)
Do đó\(\Delta ABD\)là tam giác vuông theo định lí Pytago đảo.
b) Vì \(\Delta ABD\)là tam giác vuông nên \(OB \bot AE\)nên B là trung điểm của AE.
Mặt khác \(BH//AF\)nên theo tính chất đường trung bình ta có H là trung điểm của EF\\(\widehat {OHF} = {90^0} = \widehat {OBE}\)\(OBEH\)nội tiếp (ĐPCM).
c) Ta có: \(\widehat {CHS} = \widehat {BHE}.\)Vì OBEH nội tiếp nên \(\widehat {BHE} = \widehat {BOE} = \widehat {BOA} = \widehat {COS}\)
\( \Rightarrow \) OHCS nội tiếp.
\( \Rightarrow \)\(\widehat {SCO} = \widehat {SHO} = {90^0}\).Từ đây ta có SC là tiếp tuyến của (O) (ĐPCM).
Lời giải
Giả sử tồn tại các số nguyên a,b thoả mãn đề bài.
Khi đó \({(a + b\sqrt {2023} )^2} = 2024 + 2023\sqrt {2023} \)
\(\begin{array}{l} \Rightarrow {a^2} + 2ab.\sqrt {2023} + 2023{b^2} = 2024 + 2023\sqrt {2023} \\ \Rightarrow {a^2} + 2023{b^2} - 2024 = 2023\sqrt {2023} - 2ab.\sqrt {2023} \\ \Rightarrow {a^2} + 2023{b^2} - 2024 = \sqrt {2023} (2023 - 2ab)\end{array}\)
Vì \({a^2} + 2023{b^2} - 2024\) là số hữu tỉ, còn \(\sqrt {2023} \left( {2023 - 2ab} \right)\) là số vô tỉ nên
\(2ab = 2023\). Điều này là vô lí vì 1 vế là chẵn 1 vế là lẻ.Suy ra giả sử trên sai.Vậy không tồn tại các số nguyên a,b thoả mãn đề bài.
Lời giải
Ta có: \({P_1}\left( x \right) = a{x^2} + bx + c + a\)
\({P_2}\left( x \right) = a{x^2} + bx + c + 2a\)
………………………………….
\({\rm{\;}}{P_n}\left( x \right) = a{x^2} + bx + c + na\) với n thuộc N*
Xét phương trình: \(a{x^2} + bx + c + na = 0\)
\(\Delta = {b^2} - 4a\left( {c + na} \right)\).
Chọn số nguyên dương n sao cho \(n > \frac{{{b^2} - 4ac}}{{4{a^2}}}\) , khi đó \(\Delta < 0\).Do đó phương trình \(a{x^2} + bx + c + na = 0\)vô nghiệm.Vậy cứ làm như vậy thì đến một lúc nào đó ta sẽ nhận được một đa thức không có nghiệm.