Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 28
52 người thi tuần này 4.6 112 lượt thi 8 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1) (0,5 điểm) \(A = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} = 11\sqrt 3 \)
2) (0,5 điểm) (\[P = \left( {\frac{3}{{\sqrt x - 3}} - \frac{1}{{\sqrt x + 3}}} \right).\left( {\frac{{\sqrt x }}{2} - \frac{9}{{\sqrt {4x} }}} \right) - 1\] (với x > 0, x ¹ 9)
= \[\frac{{3\sqrt x + 9 - \sqrt x - 3}}{{x - 9}}.\frac{{x - 9}}{{2\sqrt x }} - 1\] = \[\frac{{2\sqrt x + 6}}{{2\sqrt x }} - 1\]
= \[\frac{{\sqrt x + 3}}{{\sqrt x }} - 1 = \frac{{\sqrt x + 3 - \sqrt x }}{{\sqrt x }} = \frac{3}{{\sqrt x }}\].
Vậy P = \[\frac{3}{{\sqrt x }}\] với x > 0, x ¹ 9
3) (0,5 điểm) Giải hệ phương trình NH-2024-GV48: \(\left\{ \begin{array}{l} - 2x + 6y = 8\,\,\,\,\,\\3x - 7y = - 10\,\end{array} \right.\)
\(\left\{ \begin{array}{l} - 6x + 18y = 24\,\,\,\,\\6x - 14y = - 20\,\end{array} \right.\) \(\left\{ \begin{array}{l}4y = 4\,\,\,\,\\6x - 14y = - 20\,\end{array} \right.\) \(\left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\)
Vậy hệ phương trình NH-2024-GV48 có nghiệm là \(x = - 1\); \(y = 1\).Lời giải
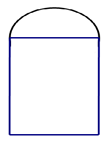
Gọi đường kính của nửa hình tròn là \[x\,(m;\,\,0 < x < 8)\]
Khi đó bán kính: \[\frac{x}{2}\,(m)\]
Gọi cạnh còn lại của hình chữ nhật là \[y\,\,(m;\,0 < y < 8)\]
khi đó tổng độ dài của khuôn gỗ
\[\begin{array}{l}\frac{{\pi x}}{2} + x + 2y = 8\\\left( {\frac{\pi }{2} + 1} \right)x + 2y = 8\\y = 4 - \left( {\frac{{\pi + 2}}{4}} \right)x\end{array}\]
S cửa sổ \[S = \frac{1}{2}\pi .{\left( {\frac{x}{2}} \right)^2} + xy = \frac{{\pi {x^2}}}{8} + xy\]
\[\frac{{\pi {x^2}}}{8} + x\left[ {4 - \left( {\frac{{\pi + 2}}{4}} \right)x} \right]\]
= … = \[ - \frac{{\pi + 4}}{8}{\left( {x - \frac{{16}}{{\pi + 4}}} \right)^2} + \frac{{32}}{{\pi + 4}} \le \frac{{32}}{{\pi + 4}}\]
Dấu “=” xảy ra khi và chỉ khi \[x = \frac{{18}}{{\pi + 4}}\] nên \[y = \frac{8}{{\pi + 4}}\]
Đoạn văn 1
Lời giải
a) (0,5 điểm) Tần số tương đối của các nhóm lần lượt là: \({f_1} = \frac{{8.100}}{{60}}\% = 13,33\% ;{f_2} = \frac{{18.100}}{{60}}\% = 30\% \)
\({f_3} = \frac{{24.100}}{{60}}\% = 40\% ;{f_4} = \frac{{10.100}}{{60}}\% = 16,67\% \)
b) (0,5 điểm) Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó
|
Nhóm |
\(\left[ {10;20} \right)\) |
\(\left[ {20;30} \right)\) |
\(\left[ {30;40} \right)\) |
\[{\rm{[}}40;50]\] |
Cộng |
|
Tần số tương đối \(\left( \% \right)\) |
\[13,33\] |
\[30\] |
\[40\] |
\[16,67\] |
\(100\) |
c) (0,5 điểm)
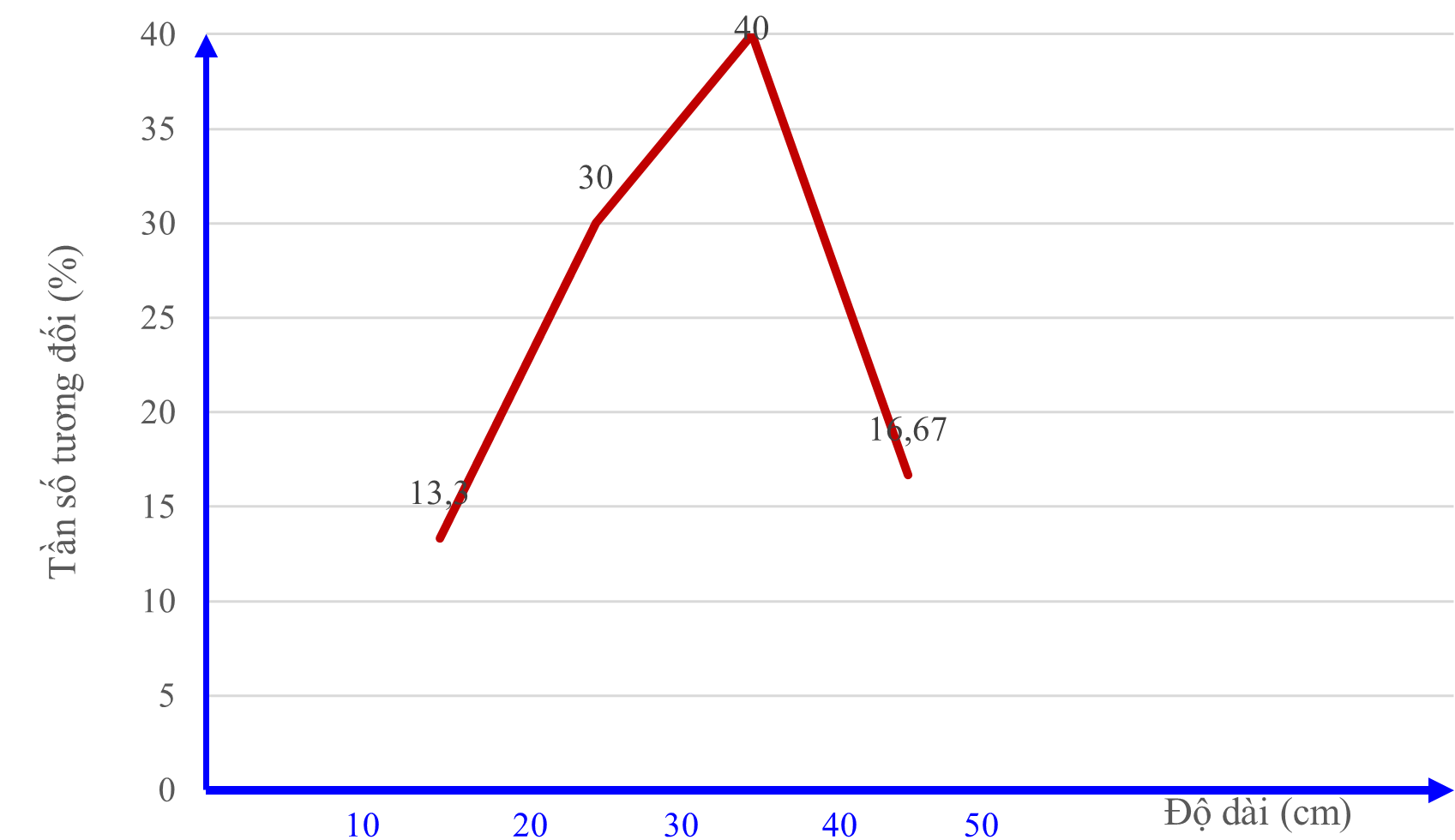
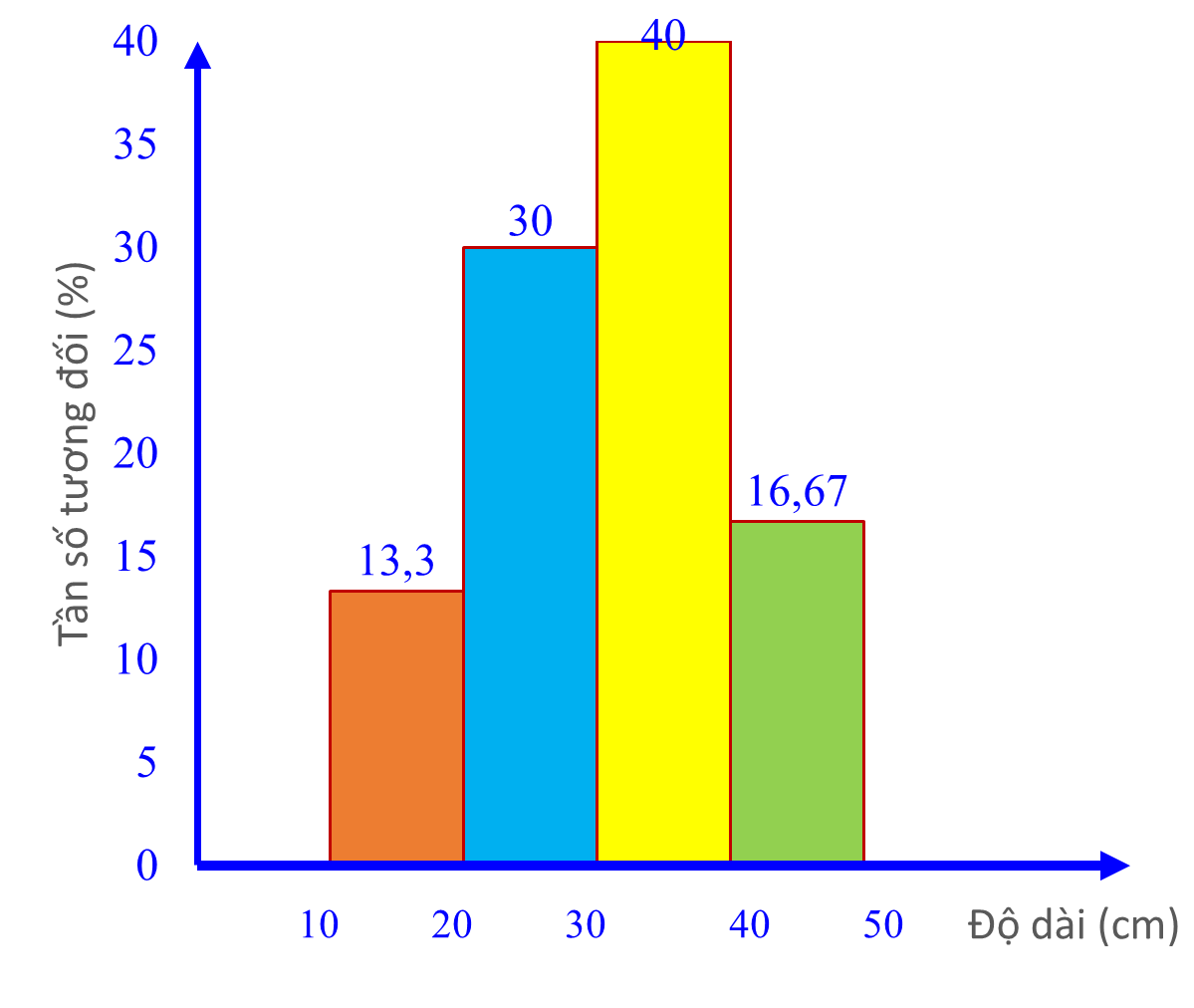
Lời giải
PT: \({x^2} - 5x - 6 = 0\) có hai nghiệm \({x_1};{x_2}\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 5}\\{{x_1}.{x_2} = - 6}\end{array}} \right.\)
Khi đó: A = \(\frac{{{x_1}}}{{{x_2} - 1}} + \frac{{{x_2}}}{{{x_1} - 1}}\) = \(\frac{{{x_1}\left( {{x_1} - 1} \right) + {x_2}\left( {{x_2} - 1} \right)}}{{\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right)}}\)
A = \(\frac{{{x_1}^2 + {x_2}^2 - \left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1}}\) = \(\frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1}}\)
Vậy: A = \(\frac{{{5^2} - 2.( - 6) - 5}}{{ - 6 - 5 + 1}} = \frac{{ - 16}}{5}\)
Đoạn văn 2
(2,0 điểm) .
Lời giải
Vì chỉ số của Zn và H ở hai bên phương trình phản ứng bằng nhau, nên ta chỉ quan tâm đến chỉ số của N và O
Theo định luật bảo toàn nguyên tố đối với N và O, ta có hệ phương trình:
\[\left\{ \begin{array}{l}4y = 2x + 2\\12y = 6x + 2 + 2y\end{array} \right.\] (0,25 điểm)
\[\left\{ \begin{array}{l}4y - 2x = 2\\10y - 6x = 2\end{array} \right.\]
\[\left\{ \begin{array}{l}2y - x = 1\,\,\,\,\,\,\,\,\left( 1 \right)\\5y - 3x = 1\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]
Nhân \[2\] vế pt \[\left( 1 \right)\]với \[3\] ta được hệ pt: \[\left\{ \begin{array}{l}6y - 3x = 3\,\,\,\,\,\,\,\,\\5y - 3x = 1\,\,\,\,\,\,\end{array} \right.\]
Trừ từng vế \[2\] pt trên ta được \[y = 2\]
Thay \[y = 2\] vào pt \[\left( 1 \right)\]ta được \[x = 3\]
Vậy ta có phương trình sau cân bằng \[3Zn + 8HN{O_3} \to 3Zn{(N{O_3})_2} + 2NO + 4{H_2}O\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.