(2,0 điểm)

Sau khi thống kê độ dài (đơn vị: centimét) của \[60\] lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau

Nhóm	\(\left[ {10;20} \right)\)	\(\left[ {20;30} \right)\)	\(\left[ {30;40} \right)\)	\[{\rm{[}}40;50]\]	Cộng
Tần số \(\left( n \right)\)	\[8\]	\[18\]	\[24\]	\[10\]	\(60\)

a) Tìm tần số tương đối của mỗi nhóm.

b) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.

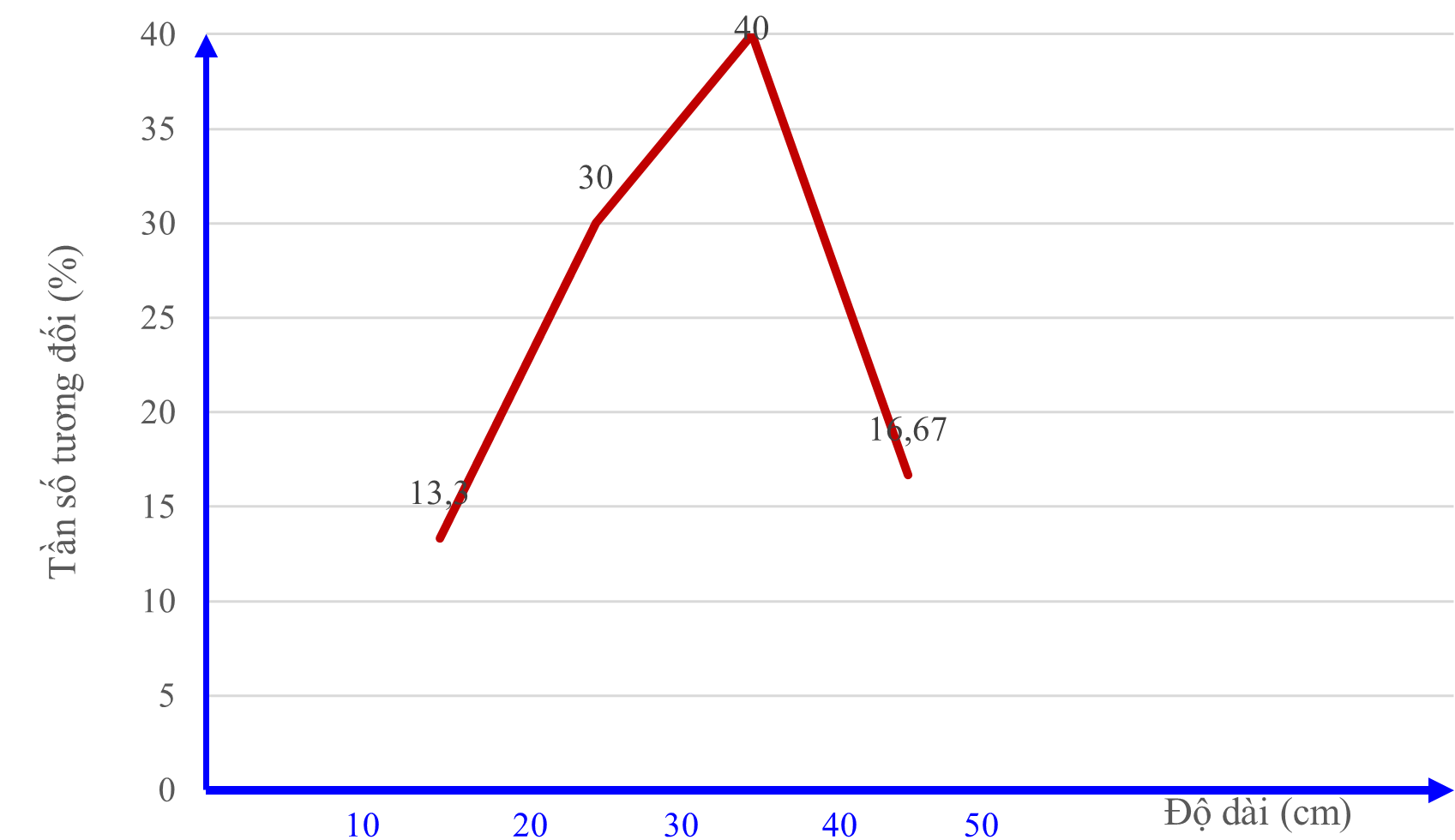
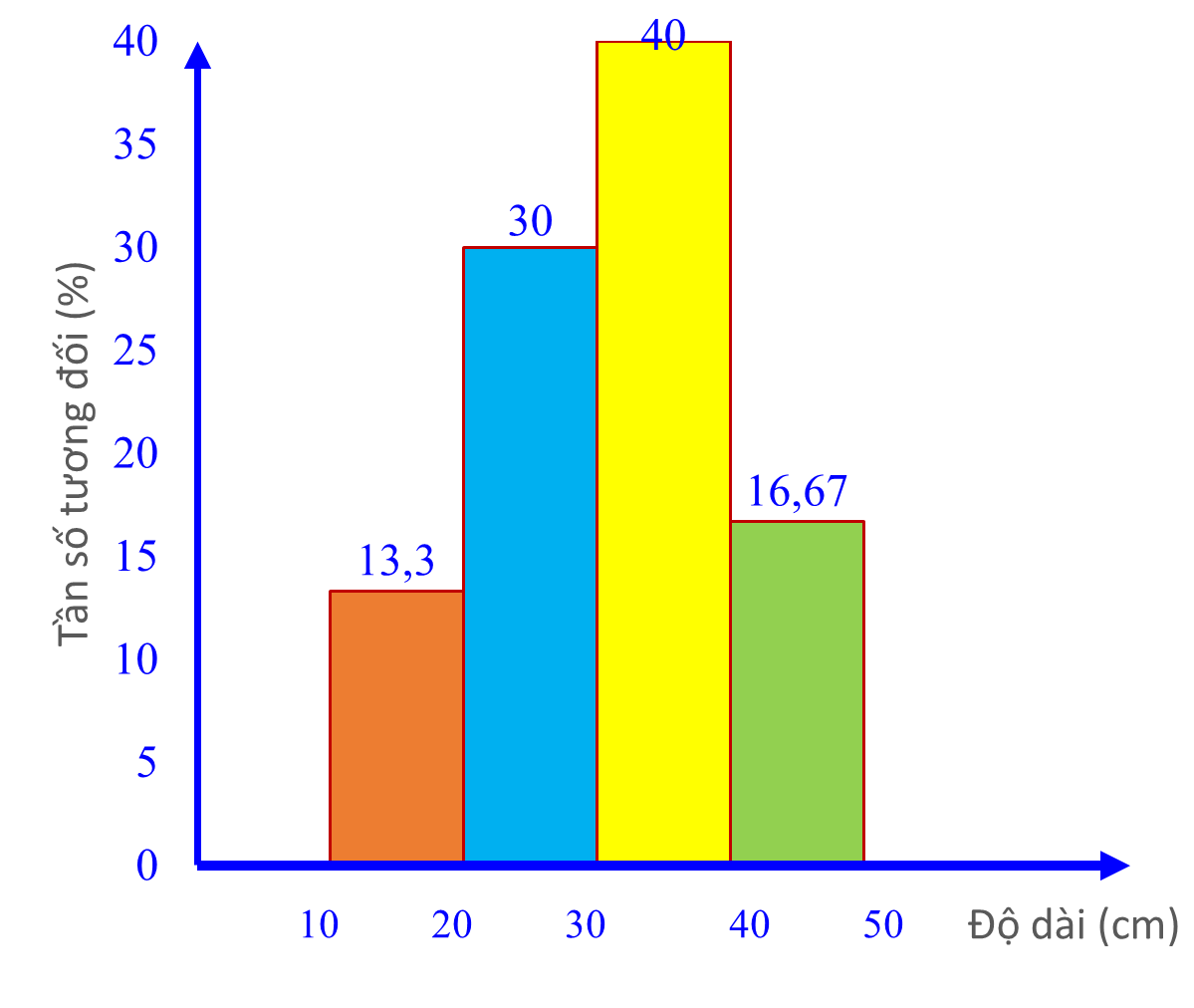
c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.

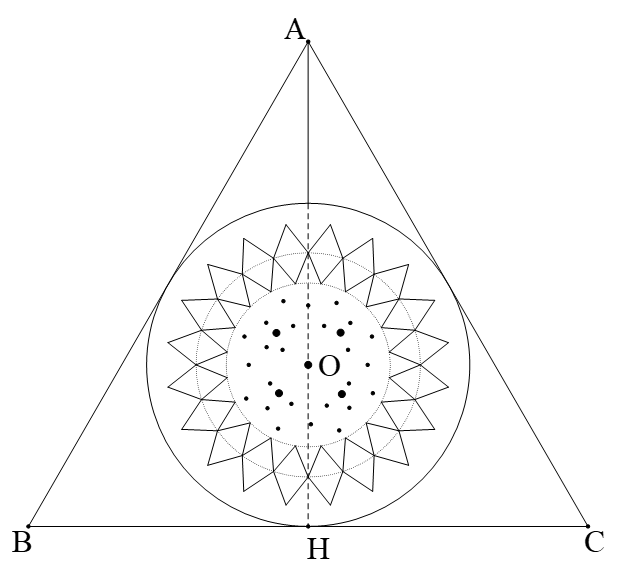
Gọi \[O\] là tâm đường tròn nội tiếp \[\Delta ABC\].

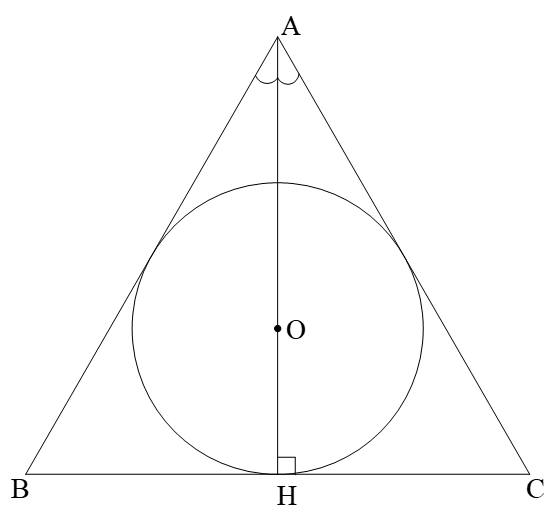
Khi đó \[O\] là giao điểm 3 đường phân giác.

Mà \[\Delta ABC\] đều nên \[AH\]là  đường phân giác cũng là đường cao, đường trung tuyến.

 Do đó \[O\] là trọng tâm \[\Delta ABC\] và  \[AH = 3.OH = 3.R\].

và \[\widehat {HAC} = \frac{{\widehat {BAC}}}{2} = {30^0};\,\,BC = 2.HC\]

Xét \[\Delta HAC\]vuông tại \[H\]ta có

\[HC = AH.\tan 30^\circ  = 3R.\frac{{\sqrt 3 }}{3} = R.\sqrt 3 \]

\[{S_{ABC}} = \frac{1}{2}AH.BC = AH.HC = 3R.R\sqrt 3 {\rm{  = 3}}\sqrt 3 {R^2}\]

\[1\,200\,\, = \,\,3\sqrt 3 .{R^2}\,\]

\[R{\rm{ = }}\sqrt {\frac{{1200}}{{3\sqrt 3 }}} \,\, \approx 15,2\,\,\,\,\,\left( {\rm{m}} \right)\]

Chu vi đường tròn (O) là \[2.3,14.15,2 \approx 95,5\](m)

               Vậy bán kính \[\left( O \right)\]là \[15,2\]m; chu vi là \[95,5\]m.

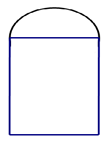
      Gọi đường kính của nửa hình tròn là  \[x\,(m;\,\,0 < x < 8)\]

 Khi đó bán kính: \[\frac{x}{2}\,(m)\]

     Gọi cạnh còn lại của hình chữ nhật là \[y\,\,(m;\,0 < y < 8)\]

    khi đó tổng độ dài của khuôn gỗ

    \[\begin{array}{l}\frac{{\pi x}}{2} + x + 2y = 8\\\left( {\frac{\pi }{2} + 1} \right)x + 2y = 8\\y = 4 - \left( {\frac{{\pi  + 2}}{4}} \right)x\end{array}\]

  S cửa sổ   \[S = \frac{1}{2}\pi .{\left( {\frac{x}{2}} \right)^2} + xy = \frac{{\pi {x^2}}}{8} + xy\]

\[\frac{{\pi {x^2}}}{8} + x\left[ {4 - \left( {\frac{{\pi  + 2}}{4}} \right)x} \right]\]

    = … =  \[ - \frac{{\pi  + 4}}{8}{\left( {x - \frac{{16}}{{\pi  + 4}}} \right)^2} + \frac{{32}}{{\pi  + 4}} \le \frac{{32}}{{\pi  + 4}}\]    

Dấu “=” xảy ra khi và chỉ khi   \[x = \frac{{18}}{{\pi  + 4}}\]  nên  \[y = \frac{8}{{\pi  + 4}}\]