(1,5 điểm)
1). Tính giá trị biểu thức \(A = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} \)
2). Rút gọn biểu thức \[P = \left( {\frac{3}{{\sqrt x - 3}} - \frac{1}{{\sqrt x + 3}}} \right).\left( {\frac{{\sqrt x }}{2} - \frac{9}{{\sqrt {4x} }}} \right) - 1\] với x > 0, x ¹ 9
3). Giải hệ phương trình : \(\left\{ \begin{array}{l}x + 2y = 1\\2x + y = 5\end{array} \right.\)
(1,5 điểm)
1). Tính giá trị biểu thức \(A = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} \)
2). Rút gọn biểu thức \[P = \left( {\frac{3}{{\sqrt x - 3}} - \frac{1}{{\sqrt x + 3}}} \right).\left( {\frac{{\sqrt x }}{2} - \frac{9}{{\sqrt {4x} }}} \right) - 1\] với x > 0, x ¹ 9
3). Giải hệ phương trình : \(\left\{ \begin{array}{l}x + 2y = 1\\2x + y = 5\end{array} \right.\)Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 28 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) (0,5 điểm) \(A = 2\sqrt {48} + 3\sqrt {75} - 2\sqrt {108} = 11\sqrt 3 \)
2) (0,5 điểm) (\[P = \left( {\frac{3}{{\sqrt x - 3}} - \frac{1}{{\sqrt x + 3}}} \right).\left( {\frac{{\sqrt x }}{2} - \frac{9}{{\sqrt {4x} }}} \right) - 1\] (với x > 0, x ¹ 9)
= \[\frac{{3\sqrt x + 9 - \sqrt x - 3}}{{x - 9}}.\frac{{x - 9}}{{2\sqrt x }} - 1\] = \[\frac{{2\sqrt x + 6}}{{2\sqrt x }} - 1\]
= \[\frac{{\sqrt x + 3}}{{\sqrt x }} - 1 = \frac{{\sqrt x + 3 - \sqrt x }}{{\sqrt x }} = \frac{3}{{\sqrt x }}\].
Vậy P = \[\frac{3}{{\sqrt x }}\] với x > 0, x ¹ 9
3) (0,5 điểm) Giải hệ phương trình NH-2024-GV48: \(\left\{ \begin{array}{l} - 2x + 6y = 8\,\,\,\,\,\\3x - 7y = - 10\,\end{array} \right.\)
\(\left\{ \begin{array}{l} - 6x + 18y = 24\,\,\,\,\\6x - 14y = - 20\,\end{array} \right.\) \(\left\{ \begin{array}{l}4y = 4\,\,\,\,\\6x - 14y = - 20\,\end{array} \right.\) \(\left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\)
Vậy hệ phương trình NH-2024-GV48 có nghiệm là \(x = - 1\); \(y = 1\).Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \[O\] là tâm đường tròn nội tiếp \[\Delta ABC\].
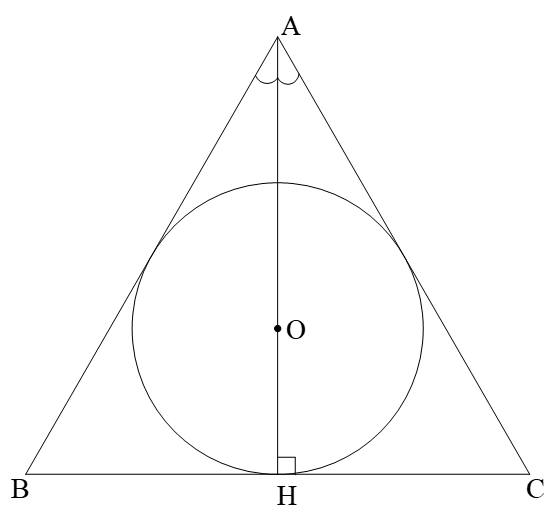
Khi đó \[O\] là giao điểm 3 đường phân giác.
Mà \[\Delta ABC\] đều nên \[AH\]là đường phân giác cũng là đường cao, đường trung tuyến.
Do đó \[O\] là trọng tâm \[\Delta ABC\] và \[AH = 3.OH = 3.R\].
và \[\widehat {HAC} = \frac{{\widehat {BAC}}}{2} = {30^0};\,\,BC = 2.HC\]
Xét \[\Delta HAC\]vuông tại \[H\]ta có
\[HC = AH.\tan 30^\circ = 3R.\frac{{\sqrt 3 }}{3} = R.\sqrt 3 \]
\[{S_{ABC}} = \frac{1}{2}AH.BC = AH.HC = 3R.R\sqrt 3 {\rm{ = 3}}\sqrt 3 {R^2}\]
\[1\,200\,\, = \,\,3\sqrt 3 .{R^2}\,\]
\[R{\rm{ = }}\sqrt {\frac{{1200}}{{3\sqrt 3 }}} \,\, \approx 15,2\,\,\,\,\,\left( {\rm{m}} \right)\]
Chu vi đường tròn (O) là \[2.3,14.15,2 \approx 95,5\](m)
Vậy bán kính \[\left( O \right)\]là \[15,2\]m; chu vi là \[95,5\]m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
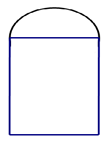
Gọi đường kính của nửa hình tròn là \[x\,(m;\,\,0 < x < 8)\]
Khi đó bán kính: \[\frac{x}{2}\,(m)\]
Gọi cạnh còn lại của hình chữ nhật là \[y\,\,(m;\,0 < y < 8)\]
khi đó tổng độ dài của khuôn gỗ
\[\begin{array}{l}\frac{{\pi x}}{2} + x + 2y = 8\\\left( {\frac{\pi }{2} + 1} \right)x + 2y = 8\\y = 4 - \left( {\frac{{\pi + 2}}{4}} \right)x\end{array}\]
S cửa sổ \[S = \frac{1}{2}\pi .{\left( {\frac{x}{2}} \right)^2} + xy = \frac{{\pi {x^2}}}{8} + xy\]
\[\frac{{\pi {x^2}}}{8} + x\left[ {4 - \left( {\frac{{\pi + 2}}{4}} \right)x} \right]\]
= … = \[ - \frac{{\pi + 4}}{8}{\left( {x - \frac{{16}}{{\pi + 4}}} \right)^2} + \frac{{32}}{{\pi + 4}} \le \frac{{32}}{{\pi + 4}}\]
Dấu “=” xảy ra khi và chỉ khi \[x = \frac{{18}}{{\pi + 4}}\] nên \[y = \frac{8}{{\pi + 4}}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập