Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 3
4.6 0 lượt thi 11 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
Đề minh họa thi vào lớp 10 môn Toán năm 2026 TP. Hồ Chí Minh
1 K lượt thi
7 câu hỏi
Đề thi tuyển sinh vào lớp 10 Toán năm học 2023 - 2024 Sở GD&ĐT Hà Nội có đáp án
670 lượt thi
7 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
4.1 K lượt thi
123 câu hỏi
67 bài tập Căn thức và các phép toán căn thức có lời giải
1 K lượt thi
67 câu hỏi
45 bài tập Phương trình quy về phương trình bậc nhất 2 ẩn và hệ phương trình bậc nhất 2 ẩn có lời giải
1.4 K lượt thi
45 câu hỏi
52 bài tập Hệ thức lượng trong tam giác có lời giải
1.9 K lượt thi
52 câu hỏi
52 bài tập Hệ Phương trình bậc nhất hai ẩn và giải hệ phương trình bậc nhất hai ẩn có lời giải
1.2 K lượt thi
52 câu hỏi
63 bài tập Tỉ số lượng giác và ứng dụng có lời giải
1.7 K lượt thi
63 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Đoạn văn 1
(1,5 điểm)
Lời giải
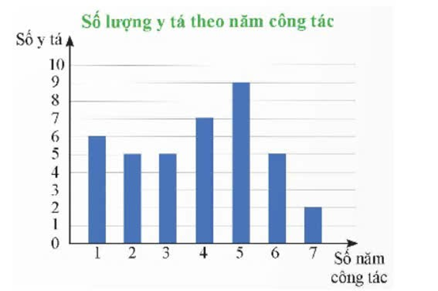
a) Các y tá của phòng khám có thời gian công tác nhận những giá trị sau\[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7.\] Bảng tần số:
|
Số năm công tác |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Số y tá |
6 |
5 |
5 |
7 |
9 |
5 |
2 |
b) Phòng khám có: \[6 + 5 + 5{\rm{ }} + 7 + 9 + 5{\rm{ }} + 2{\rm{ }} = 39\]y tá.
c) Có \[5 + 7 + 9 + 5 + 2 = 28\]y tá đã công tác ở phòng khám ít nhất 3 năm.
Lời giải
a) Các kết quả có thể xảy ra là: Trung, Quý, Việt, An, Châu, Hương.
b) Có 3 kết quả thuận lợi cho biến cố A là: An, Châu, Hương.
Vậy \[P\left( A \right) = \frac{3}{6} = \frac{1}{2}\].
Có 3 kết quả thuận lợi cho biến cố B là: Trung, Quý, An.
Vậy \[P\left( B \right) = \frac{3}{6} = \frac{1}{2}\].
Đoạn văn 2
(1,5 điểm) Cho hai biểu thức \(A = \frac{{x - 7}}{{\sqrt x }}\)và \(B = \frac{1}{{\sqrt x + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{2x - \sqrt x + 2}}{{x - 4}}\) với \(x > 0,x \ne 4\)
Lời giải
Thay x = 9 ( tmđk) vào biểu thức \[A\], ta được:
\(A = \frac{{9 - 7}}{{\sqrt 9 }} = \frac{2}{3}\)
Vậy khi \(x = 9\)thì \(A = \frac{2}{3}\)
Lời giải
\(B = \frac{1}{{\sqrt x + 2}} - \frac{{\sqrt x }}{{\sqrt x - 2}} + \frac{{2x - \sqrt x + 2}}{{x - 4}}\)
\(\begin{array}{l} = \frac{{\sqrt x - 2 - \sqrt x \left( {\sqrt x + 2} \right) + 2x - \sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}\\ = \frac{{\sqrt x - 2 - x - 2\sqrt x + 2x - \sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt {x - 2} } \right)}}\\ = \frac{{x - 2\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x \left( {\sqrt {x - 2} } \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x }}{{\sqrt x + 2}}\end{array}\)
Vậy \(B = \frac{{\sqrt x }}{{\sqrt x + 2}}\) với \(x > 0,x \ne 4\)
Lời giải
\(P = \frac{{x - 7}}{{\sqrt x }}.\frac{{\sqrt x }}{{\sqrt x + 2}} = \frac{{x - 7}}{{\sqrt x + 2}}\)+ Xét \(P = \frac{{x - 7}}{{\sqrt x }}.\frac{{\sqrt x }}{{\sqrt x + 2}} = \frac{{x - 7}}{{\sqrt x + 2}}\) ( thoả mãn đk )
+ Xét \(P \ne 0\)
TH1: \(x \in \mathbb{Z};x \ne 7;\sqrt x \)là số vô tỉ \(P \notin \mathbb{Z}\) ( loại)
TH2: \(x \in \mathbb{Z},\sqrt x \in \mathbb{Z}\)
Ta có: \(P = \frac{{x - 4 - 3}}{{\sqrt {x + 2} }} = \frac{{x - 4}}{{\sqrt x + 2}} - \frac{3}{{\sqrt x + 2}} = \sqrt x - 2 - \frac{3}{{\sqrt x + 2}}\)
Để \(P \in \mathbb{Z}\)
Suy ra \(\sqrt x - 2 - \frac{3}{{\sqrt x + 2}} \in \mathbb{Z}\)
Suy ra \(\frac{3}{{\sqrt x + 2}} \in \mathbb{Z}\)
Suy ra \(\sqrt x + 2 \in \)Ư(3)
Vậy \(\sqrt x + 2 \in \left\{ {1;3} \right\}\)
Do \(\sqrt x + 2 \ge 2 \Leftrightarrow \sqrt x + 2 = 3 \Leftrightarrow \sqrt x = 1 \Leftrightarrow x = 1\) ( thoả mãn )
Vậy với \(x \in \left\{ {1;7} \right\}\); thì P có giá trị nguyên
Đoạn văn 3
(2,5 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(4,0 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập