Đề thi minh họa Toán vào 10 năm học 2025 - 2026 Thái Bình

1) Thay \(x = 9\) (thoả mãn điều kiện \(x \ge 0,\,\,x \ne 1)\) vào biểu thức \[B\] ta được:

\(B = \frac{{\sqrt 9  - 1}}{{\sqrt 9  + 1}} = \frac{2}{4} = \frac{1}{2}.\)

Vậy khi \(x = 9\) thì \(B = \frac{1}{2}.\)

2) Với \(x \ge 0,\,\,x \ne 1,\) ta có:

\(A = \frac{{\sqrt x }}{{\sqrt x  - 1}} - \frac{2}{{\sqrt x  + 2}} + \frac{{4\sqrt x  + 2}}{{x + \sqrt x  - 2}}\)

 \( = \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{2\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} + \frac{{4\sqrt x  + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

 \( = \frac{{x + 2\sqrt x  - 2\sqrt x  + 2 + 4\sqrt x  + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

 \( = \frac{{x + 4\sqrt x  + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

 \( = \frac{{{{\left( {\sqrt x  + 2} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{\sqrt x  + 2}}{{\sqrt x  - 1}}.\)

Vậy \(A = \frac{{\sqrt x  + 2}}{{\sqrt x  - 1}}.\)

3) Với \(x \ge 0,\,\,x \ne 1,\) ta có:

\(T = 4 - \frac{3}{2}AB = 4 - \frac{3}{2} \cdot \frac{{\sqrt x  + 2}}{{\sqrt x  - 1}} \cdot \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} = 4 - \frac{3}{2} \cdot \frac{{\sqrt x  + 2}}{{\sqrt x  + 1}}\)

 \[ = \frac{{4 \cdot 2\left( {\sqrt x  + 1} \right) - 3\left( {\sqrt x  + 2} \right)}}{{2\left( {\sqrt x  + 1} \right)}}\]\[ = \frac{{8\sqrt x  + 8 - 3\sqrt x  - 6}}{{2\left( {\sqrt x  + 1} \right)}}\]

 \( = \frac{{5\sqrt x  + 2}}{{2\left( {\sqrt x  + 1} \right)}} = \frac{{5\left( {\sqrt x  + 1} \right) - 3}}{{2\left( {\sqrt x  + 1} \right)}} = \frac{5}{2} - \frac{3}{{2\left( {\sqrt x  + 1} \right)}}.\)

Với \(x \ge 0,\,\,x \ne 1\) thì \(\sqrt x  + 1 > 0\) nên \(\frac{3}{{2\left( {\sqrt x  + 1} \right)}} > 0\) suy ra \(\frac{5}{2} - \frac{3}{{2\left( {\sqrt x  + 1} \right)}} < \frac{5}{2}.\)

Vì \[T\] nhận giá trị nguyên lớn nhất nên \(T = 2,\) tức là \(\frac{{5\sqrt x  + 2}}{{2\left( {\sqrt x  + 1} \right)}} = 2,\) suy ra \(5\sqrt x  + 2 = 4\sqrt x  + 4\) hay \(\sqrt x  = 2,\) ta tìm được \(x = 4\) (thoả mãn điều kiện \(x \ge 0,\,\,x \ne 1).\)

Vậy khi \(x = 4\) thì \[T\] đạt giá trị nguyên lớn nhất.

1) Đối tượng thống kê là: Mặt 1 chấm, Mặt 2 chấm, Mặt 3 chấm, Mặt 4 chấm, Mặt 5 chấm, Mặt 6 chấm.

Kích thước mẫu thống kê là: 20.

Xét phép thử: “Chọn ngẫu nhiên một học sinh của lớp 9A”.

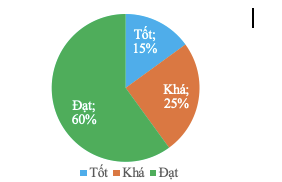
Tỷ lệ học sinh xếp loại học tập Khá, Tốt là \(25\%  + 15\%  = 40\% .\)

Gọi tổng số học sinh có xếp loại học tập Khá, Tốt là \[40k,\] số học sinh cả lớp là \[100k\,\,\left( {40k \in {\mathbb{N}^*};\,\,100k \in {\mathbb{N}^*}} \right).\]

Suy ra kích thước của không gian mẫu trong phép thử trên là \[100k.\]

Gọi \[A\] là biến cố “Chọn được học sinh có xếp loại học tập Khá hoặc Tốt” thì số kết quả thuận lợi cho biến cố A là \[40k.\]

Vì các kết quả có thể trong phép thử trên là đồng khả năng nên xác suất của biến cố \[A\] là \(P\left( A \right) = \frac{{40k}}{{100k}} = 40\% .\)

Gọi bán kính của khối cầu là \(r{\rm{\;(m)}},\,\,r > 0.\)

Khi đó:

⦁ Diện tích mặt cầu của khối cầu là: \[S = 4\pi {r^2}{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]

⦁ Thể tích của khối cầu là: \(V = \frac{4}{3}\pi {r^3}{\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)

Vì giá trị diện tích mặt cầu (tính bằng m2) gấp 3 lần giá trị thể tích của khối cầu đó (tính bằng m3) nên ta có:

\(4\pi {r^2} = 3 \cdot \frac{4}{3}\pi {r^3},\) suy ra \(r = 1{\rm{\;(m)}}{\rm{.}}\)

Do đó thể tích của khối cầu là \(V = \frac{4}{3} \cdot 3,14 \cdot {1^3} = \frac{{314}}{{75}}{\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)

Vậy khối lượng của khối cầu sắt là: \(m = \frac{{314}}{{75}} \cdot 7\,\,800 = 32\,\,656\,\,({\rm{kg}}).\)

Gọi giá niêm yết của đôi giày và chiếc vợt lần lượt là \(x,\,\,y\) triệu đồng \[\left( {x,\,\,y > 0} \right).\]

Vì tổng số tiền theo giá niêm yết của hai mặt hàng là 2,4 triệu đồng nên ta có phương trình: \(x + y = 2,4.\)

Giá 1 đôi giày thể thao sau giảm giá là: \(x - 10\% x = 90\% x = 0,9x\) (triệu đồng).

Giá 1 chiếc vợt sau giảm giá là: \(y - 15\% y = 85\% y = 0,85y\) (triệu đồng).

Vì anh Khánh trả cho cửa hàng 3,2 triệu đồng khi mua 1 đôi giày thể thao và 2 chiếc vợt theo chương trình khuyến mại nên ta có phương trình: \(0,9x + 2 \cdot 0,85y = 3,2.\)

Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 2,4}\\{0,9x + 2 \cdot 0,85y = 3,2}\end{array}} \right..\)

Giải hệ phương trình trên, ta được: \(\left\{ {\begin{array}{*{20}{l}}{x = 1,1}\\{y = 1,3}\end{array}} \right.\). Các giá trị thoả mãn điều kiện.

Vậy giá niêm yết của đôi giày là 1,1 triệu đồng, của chiếc vợt là 1,3 triệu đồng.

Xét parabol \(y = m{x^2}\,\,\left( {m < 0} \right)\) trong mặt phẳng tọa đô \[Oxy\] như hình vẽ.

Vì Parabol nhận \[Oy\]làm trục đối xứng nên \(HB = 4\;{\rm{m}}\) hay \(OE = 4\;{\rm{m}}\)

Độ cao của cổng là 6 m nên \(OH = 6\;{\rm{m}}\) suy ra \(B\left( {4;\,\, - 6} \right)\)

Vì \(B\) thuộc parabol nên ta có \( - 6 = m \cdot {4^2}\) hay \(m = \frac{{ - 3}}{8}.\) Suy ra \(y = \frac{{ - 3}}{8}{x^2}.\)

Thanh sắt đặt nằm ngang ở độ cao \(4,5\;\;{\rm{m}}\) so với mặt đất nên ta có \(IH = 4,5\;{\rm{m}}\) suy ra \(OI = OH - IH = 6 - 4,5 = 1,5{\rm{\;(m)}}{\rm{.}}\)

Đặt \[OF = x\,\,({\rm{m}});\,\,\,x > 0.\]

Ta có \(D\left( {x; - 1,5} \right)\) thuộc parabol nên \( - 1,5 = \frac{{ - 3}}{8}{x^2}.\) Suy ra \(x = 2.\)

Hay \[ID = 2\;{\rm{m}}{\rm{.}}\] Suy ra \(CD = 4\;{\rm{m}}{\rm{.}}\)

Vậy độ dài của thanh sắt là 4 m.