Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Tây Ninh có đáp án

Ta có: \(T = \sqrt {13 + 4\sqrt 3 }  - \sqrt {13 - 4\sqrt 3 }  = \sqrt {12 + 2.2\sqrt 3 .1 + 1}  - \sqrt {12 - 2.2\sqrt 3 .1 + 1} \)

\( = \sqrt {{{(2\sqrt 3  + 1)}^2}}  - \sqrt {{{(2\sqrt 3  - 1)}^2}}  = \left| {2\sqrt 3  + 1\left|  -  \right|2\sqrt 3  - 1} \right| = 2\sqrt 3  + 1 - 2\sqrt 3  + 1 = 2\)

Do \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cùng đi qua điểm \(M\left( {2; - 3} \right)\) nên ta có: \(\left\{ {\begin{array}{*{20}{l}}{2a + 5 =  - 3}\\{6 + b - 2 =  - 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a =  - 4}\\{b =  - 7}\end{array}} \right.} \right.\).

Vậy \(a =  - 4;b =  - 7\)

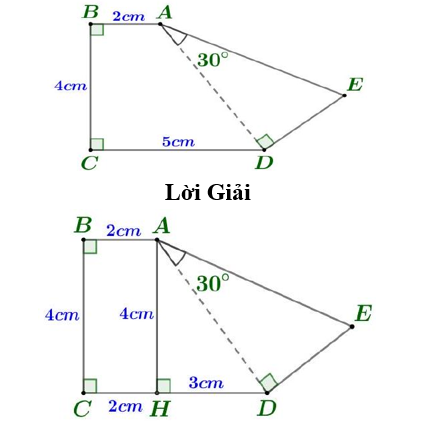
Kẻ \(AH \bot CD\).

Suy ra: \(ABCH\) là hình chữ nhật\( \Rightarrow AH = 4{\rm{\;}}cm;HD = CD - CH = 3{\rm{\;}}cm\).

Xét \({\rm{\Delta }}AHD\left( {\hat H = {{90}^ \circ }} \right)\) có: \(A{D^2} = A{H^2} + H{D^2} = {4^2} + {3^2} = 25 \Rightarrow AD = 5{\rm{\;}}cm\).

Xét \({\rm{\Delta }}ADE\left( {\widehat {ADE} = {{90}^ \circ }} \right)\) có: \(cos{30^ \circ } = \frac{{AD}}{{AE}} \Rightarrow AE = \frac{{AD}}{{cos{{30}^ \circ }}} = \frac{{10}}{{\sqrt 3 }} = \frac{{10\sqrt 3 }}{3}\).

Vậy \(AE = \frac{{10\sqrt 3 }}{3}\)

Đặt: \(\frac{{2a}}{b} = \frac{{3b}}{c} = \frac{c}{{6a}} = t \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2a = bt}\\{b = \frac{c}{3}t = 2a{t^2} \Leftrightarrow 2a = 2a{t^3} \Leftrightarrow t = 1.}\\{c = 6at}\end{array}} \right.\)

Suy ra: \(\left\{ {\begin{array}{*{20}{l}}{b = 2a}\\{c = 6a}\end{array}} \right.\).

\(P = \frac{{4ac - cb}}{{bc + 2ab}} = \frac{{4a.6a - 6a.2a}}{{2a.6a + 2a.2a}} = \frac{{12}}{{16}} = \frac{3}{4}\)

\({\left( {x + y} \right)^2} + 2{y^2}\left( {x + 1} \right) + {\left( {y + 2} \right)^2} - 9 = 0\left( {\rm{*}} \right)\)

\( \Leftrightarrow {x^2} + {y^2} + 2xy + 2x{y^2} + 2{y^2} + {y^2} + 4y + 4 - 9 = 0\)

\( \Leftrightarrow {x^2} - 4 + 2x\left( {{y^2} + y} \right) + 4\left( {{y^2} + y} \right) = 1\)

\( \Leftrightarrow \left( {x + 2} \right)\left( {x - 2} \right) + 2\left( {{y^2} + y} \right)\left( {x + 2} \right) = 1\)

\( \Leftrightarrow \left( {x + 2} \right)\left( {x - 2 + 2{y^2} + 2y} \right) = 1\)

TH1: \(\left\{ {\begin{array}{*{20}{c}}{x + 2 = 1}\\{x - 2 + 2{y^2} + 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - 1}\\{2{y^2} + 2y = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - 1}\\{\left[ {\begin{array}{*{20}{c}}{y = 1}\\{y =  - 2}\end{array}} \right.}\end{array}} \right. \Rightarrow \left( { - 1;1} \right),{\rm{\;}}\left( { - 1;{\rm{\;}} - 2} \right)\)

TH2: \(\left\{ {\begin{array}{*{20}{c}}{x + 2 = 1}\\{x - 2 + 2{y^2} + 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - 3}\\{2{y^2} + 2y = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - 3}\\{\left[ {\begin{array}{*{20}{c}}{y = 1}\\{y =  - 2}\end{array}} \right.}\end{array}} \right. \Rightarrow \left( { - 3;1} \right),{\rm{\;}}\left( { - 3;{\rm{\;}} - 2} \right)\)