Đề thi tuyển sinh vào lớp 10 Toán năm học 2022 - 2023 Sở GD&ĐT TP.HCM có đáp án
39 người thi tuần này 4.6 150 lượt thi 8 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) Lập bảng giá trị:
|
\[x\] |
-4 |
-2 |
0 |
2 |
4 |
|
\[\left( P \right):y = \frac{1}{4}{x^2}\] |
4 |
1 |
0 |
1 |
4 |
|
\[x\] |
0 |
4 |
|
\[\left( d \right):y = - \frac{1}{2}x + 2\] |
2 |
0 |
Parabol \[\left( P \right)\] là đường cong đi qua các điểm có tọa độ \[\left( { - 4;\,4} \right),\,\left( { - 2;\,1} \right),\,\left( {0;\,0} \right)\],\[\left( {2;\,1} \right)\],\[\left( {4;\,4} \right)\].
Đường thẳng \[\left( d \right)\] đi qua hai điểm có tọa độ \[\left( {0;\,2} \right),\,\left( {4;\,0} \right)\].
Vẽ \[\left( P \right)\] và \[\left( d \right)\] trên cùng hệ trục tọa độ, ta được:
b) Hoành độ giao điểm của \[\left( d \right)\] và \[\left( P \right)\] là nghiệm của phương trình:
\[\frac{1}{4}{x^2} = - \frac{1}{2}x + 2\]
\[ \Leftrightarrow {x^2} + 2x - 8 = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 4\end{array} \right.\]
Với \[x = 2 \Rightarrow y = 1\] ta có giao điểm \[A\left( {2;\,1} \right)\].
Với \[x = - 4 \Rightarrow y = 4\] ta có giao điểm \[B\left( { - 4;\,4} \right)\].
Vậy tọa độ giao điểm của \[\left( P \right)\] và \[\left( d \right)\] là \[A\left( {2;\,1} \right)\]và \[B\left( { - 4;\,4} \right)\].
Lời giải
Ta có \[{x_1},\,{x_2}\] là nghiệm của phương trình \[2{x^2} - 5x - 3 = 0\].
Áp dụng hệ thức Vi-et ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{5}{2}\\{x_1}{x_2} = \frac{{ - 3}}{2}\end{array} \right.\]
\[A = \left( {{x_1} + 2{x_2}} \right)\left( {{x_2} + 2{x_1}} \right)\]
\[ = {x_1}{x_2} + 2x_1^2 + 2x_2^2 + 4{x_1}{x_2}\]
\[ = 2\left( {x_1^2 + x_2^2} \right) + 5{x_1}{x_2}\]
\[ = 2{\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} + 5{x_1}{x_2}\]
\[ = 2{\left( {{x_1} + {x_2}} \right)^2} + {x_1}{x_2}\]
\[ = 2.{\left( {\frac{5}{2}} \right)^2} + \left( { - \frac{3}{2}} \right) = 11\].
Lời giải
a) Ta có:
2005 : 10 = 200 dư 5 Þ CAN = “ẤT”.
2005 : 12 = 167 dư 1 Þ CHI = “DẬU”.
Vậy năm 2005 có CAN là “Ất”, CHI là “Dậu”.
b) Gọi \[x\] là năm Nguyễn Huệ lên ngôi hoàng đế \[\left( {x \in \mathbb{N}} \right)\].
Do \[x\] thuộc cuối thế kỉ 18 nên \[1750 \le x \le 1799\].
Do CAN của \[x\] là Mậu nên \[x\] : 10 dư 8.
Suy ra hàng đơn vị của \[x\] là số 8.
Suy ra \[x\] là một trong các năm 1758, 1768, 1778, 1788, 1798.
Do CHI của \[x\] là “Thân” nên \[x\] chia hết cho 12.
Vậy chỉ có năm 1788 thỏa mãn.
Vậy Nguyễn Huệ lên ngôi hoàng đế năm 1788.
Lời giải
Theo đề ta có hệ phương trình \[\left\{ \begin{array}{l}100a + b = 40\\4a + b = 28\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{5}\\b = 20\end{array} \right.\]
Vậy \[a = \frac{1}{5},\,b = 20\].
Lời giải
Gọi \[x\] là số xe mà anh Thành bán được trong tháng 5.
Theo đề ta có phương trình
\[8\,000\,000 + \left( {x - 31} \right).8\% .2\,500\,000 = \,9800\,000\]
Giải phương trình trên ta được \[x = 40\].
Vậy anh Thành bán được 40 chiếc xe máy trong tháng 5.
Lời giải
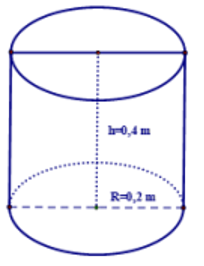
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.