Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Lai Châu có đáp án
45 người thi tuần này 4.6 96 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) \(A = \left( {\frac{{x + 4\sqrt x + 4}}{{x + \sqrt x - 2}} + \frac{{x + \sqrt x }}{{1 - x}}} \right):\left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{1 - \sqrt x }}} \right)\)
\(\)\( = \left[ {\frac{{{{\left( {\sqrt x + 2} \right)}^2}}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}} + \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {1 - \sqrt x } \right)\left( {1 + \sqrt x } \right)}}} \right]:\frac{{\sqrt x - 1 + \sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \left[ {\frac{{\sqrt x + 2}}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{1 - \sqrt x }}} \right]:\frac{{2\sqrt x }}{{\left( {1 - \sqrt x } \right)\left( {1 + \sqrt x } \right)}}\)
\( = \frac{2}{{\sqrt x - 1}}.\frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}{{2\sqrt x }} = \frac{{\sqrt x + 1}}{{\sqrt x }}\)
Vậy \(A = \frac{{\sqrt x + 1}}{{\sqrt x }}\) với \(x > 0;\,x \ne 1\).
b) \(A \ge \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }} \Leftrightarrow \frac{{\sqrt x + 1}}{{\sqrt x }} \ge \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }} \Leftrightarrow \frac{{\sqrt x + 1}}{{\sqrt x }} - \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }} \ge 0\)
\( \Leftrightarrow \frac{{\sqrt x \sqrt {2023} + \sqrt {2023} - \sqrt x - \sqrt x .\sqrt {2023} }}{{\sqrt x .\sqrt {2023} }} \ge 0 \Leftrightarrow \sqrt {2023} - \sqrt x \ge 0 \Leftrightarrow x \le 2023\)
Kết hợp điều kiện \(x > 0;\,x \ne 1\) ta có \(2022\) giá trị thỏa mãn điều kiện
Lời giải
a) \(\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\2{x^2} + {y^2} - 3xy + 3x - 2y + 1 = 0\,\,\,\left( 2 \right)\end{array} \right.\)
\[ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\\left( {x - y + 1} \right)\left( {2x - y + 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\\left[ \begin{array}{l}x - y + 1 = 0\\2x - y + 1 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\x - y + 1 = 0\end{array} \right.\,\left( * \right)\\\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\2x - y + 1 = 0\end{array} \right.\,\left( {**} \right)\end{array} \right.\]
Giải \(\left( * \right)\)\[\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\x - y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y - 1\\2{y^2} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y - 1\\\left[ \begin{array}{l}y = 2\\y = - 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\\\left\{ \begin{array}{l}x = - 3\\y = - 2\end{array} \right.\end{array} \right.\]
Giải \(\left( {**} \right)\) \[\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\2x - y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {\left( {2x + 1} \right)^2} + x + 2x + 1 = 8\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5{x^2} + 7x - 6 = 0\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x + 1\\\left[ \begin{array}{l}x = \frac{3}{5}\\x = - 2\end{array} \right.\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = \frac{3}{5}\\y = \frac{{11}}{5}\end{array} \right.\\\left\{ \begin{array}{l}x = - 2\\y = - 3\end{array} \right.\end{array} \right.\]
Vậy hệ phương trình đã cho có 4 nghiệm \(\left( {1;2} \right);\left( { - 3; - 2} \right);\left( { - 2; - 3} \right);\left( {\frac{3}{5};\frac{{11}}{5}} \right)\)
b) Xét phương trình hoành độ tương giao của \(\left( P \right)\) và \(\left( d \right)\): \({x^2} = - x + m + 1 \Leftrightarrow {x^2} + x - m - 1 = 0\,\left( * \right)\)
để \(\left( d \right)\) cắt \(\left( P \right)\) tại 2 điểm phân biệt \({x_1};{x_2}\) thì \(\left( * \right)\) có 2 nghiệm phân biệt
\( \Rightarrow \Delta > 0 \Leftrightarrow 1 + 4\left( {m + 1} \right) > 0 \Leftrightarrow m > \frac{{ - 5}}{4}\)
Ta có \({x_1}^2 - {x_2} - 4m + 1 = 0\left( 1 \right)\)
Vì \({x_1}\) là nghiệm của \(\left( * \right)\) suy ra \({x_1}^2 = - {x_1} + m + 1\) thay vào \(\left( 1 \right)\) ta được \( - {x_1} + m + 1 - {x_2} - 4m + 1 = 0 \Leftrightarrow - \left( {{x_1} + {x_2}} \right) - 3m + 2 = 0\)
Theo viet ta có: \({x_1} + {x_2} = - 1 \Rightarrow m = 1\)( nhận)
Vậy \(m = 1\) thỏa mãn đề bài.
Lời giải
a) \(\left( {2x + y} \right)\left( {x - y} \right) + x + 8y = 22 \Leftrightarrow \left( {2x + y} \right)\left( {x - y} \right) + 3\left( {2x + y} \right) - 5\left( {x - y} \right) = 22\)
\(\begin{array}{l} \Leftrightarrow \left( {2x + y} \right)\left( {x - y + 3} \right) - 5\left( {x - y + 3} \right) = 7\\ \Leftrightarrow \left( {x - y + 3} \right)\left( {2x + y - 5} \right) = 7\end{array}\)
Khi đó ta có các khả năng sau:
KN1: \(\left\{ \begin{array}{l}x - y + 3 = - 7\\2x + y - 5 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 8\end{array} \right.\)
KN2: \(\left\{ \begin{array}{l}x - y + 3 = - 1\\2x + y - 5 = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 2\end{array} \right.\)
KN3: \(\left\{ \begin{array}{l}x - y + 3 = 7\\2x + y - 5 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{10}}{3}\\y = \frac{{ - 2}}{3}\end{array} \right.\left( l \right)\)
KN4: \(\left\{ \begin{array}{l}x - y + 3 = 1\\2x + y - 5 = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{10}}{3}\\y = \frac{{16}}{3}\end{array} \right.\left( l \right)\)
Vậy nghiệm của phương trình là \(\left( {x;y} \right) \in \left\{ {\left( { - 2;8} \right);\left( { - 2;2} \right)} \right\}\)
b) ta có \(a + b + c = 3 \Leftrightarrow 9 = {\left( {a + b + c} \right)^2} \ge 3\left( {ab + ac + bc} \right) \Leftrightarrow ab + ac + bc \le 3\)
ta có \(\frac{{bc}}{{\sqrt {{a^2} + 3} }} \le \frac{{bc}}{{\left( {{a^2} + ab + ac + bc} \right)}} = \frac{{bc}}{{\sqrt {\left( {a + b} \right)\left( {a + c} \right)} }} \le \frac{1}{2}\left( {\frac{{bc}}{{a + b}} + \frac{{bc}}{{a + c}}} \right)\)
tương tự ta có : \(\frac{{ac}}{{\sqrt {{b^2} + 3} }} \le \frac{1}{2}\left( {\frac{{ac}}{{a + b}} + \frac{{ac}}{{b + c}}} \right)\);\(\frac{{ab}}{{\sqrt {{c^2} + 3} }} \le \frac{1}{2}\left( {\frac{{ab}}{{b + c}} + \frac{{ab}}{{a + c}}} \right)\)
cộng vế với vế của các bất đẳng thức trên ta được: \(\frac{{bc}}{{\sqrt {{a^2} + 3} }} + \frac{{ac}}{{\sqrt {{b^2} + 3} }} + \frac{{ab}}{{\sqrt {{c^2} + 3} }} \le \frac{1}{2}\left( {\frac{{bc}}{{a + b}} + \frac{{bc}}{{a + c}} + \frac{{ac}}{{a + b}} + \frac{{ac}}{{b + c}} + \frac{{ab}}{{b + c}} + \frac{{ab}}{{a + c}}} \right) \le \frac{1}{2}\left( {a + b + c} \right)\)
mà \(a + b + c = 3\) nên \(\frac{{bc}}{{\sqrt {{a^2} + 3} }} + \frac{{ac}}{{\sqrt {{b^2} + 3} }} + \frac{{ab}}{{\sqrt {{c^2} + 3} }} \le \frac{3}{2}\)
dấu \('' = ''\) xảy ra khi \(a = b = c = 1\)
Vậy \(\frac{{bc}}{{\sqrt {{a^2} + 3} }} + \frac{{ac}}{{\sqrt {{b^2} + 3} }} + \frac{{ab}}{{\sqrt {{c^2} + 3} }} \le \frac{3}{2}\)
Lời giải
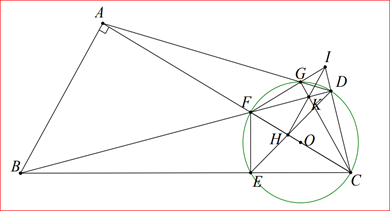
a) tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {BAC} = 90^\circ \) hay \(\widehat {BAF} = 90^\circ \)
ta có: \(FE \bot BC\) tại \(E\) nên \(\widehat {FEB} = \widehat {FEC} = 90^\circ \)
xét tứ giác \(ABEF\) có \(\widehat {BAF} + \widehat {FEB} = 180^\circ \) mà hai góc đối nhau nên \(ABEF\) là tứ giác nội tiếp
b) Xét đường tròn tâm \(\left( O \right)\) có \(\widehat {FDC} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn)
Hay \(\widehat {BDC} = 90^\circ \)
Xét tứ giác \(ABCD\) có \(\widehat {BAC} = \widehat {BDC} = 90^\circ \) mà hai đỉnh kề nên \(ABCD\) là tứ giác nội tiếp
Xét đường tròn ngoại tiếp tứ giác \(ABCD\) có \(\widehat {ABD} = \widehat {ACD}\) ( hai góc nội tiếp cùng chắn )
Hay \(\widehat {ABF} = \widehat {FCD}\) (1)
Xét đường tròn ngoại tiếp tứ giác \(ABEF\) có \[\widehat {ABF} = \widehat {AEF}\]( hai góc nội tiếp cùng chắn ) (2)
Xét đường tròn tâm \(\left( O \right)\) có \[\widehat {FCD} = \widehat {FED}\]( hai góc nội tiếp cùng chắn ) (3)
Từ (1); (2) và (3) ta có \[\widehat {FED} = \widehat {AEF}\] nên \(FE\) là tia phân giác của \(\widehat {AED}\)
Xét tam giác \(AEH\) có \[{\rm{EF;EC}}\] là đường phân giác trong và ngoài của tam giác nên \[\frac{{AF}}{{FH}} = \frac{{AE}}{{EH}};\frac{{AC}}{{CH}} = \frac{{AE}}{{EH}}\]
Suy ra \(\frac{{AF}}{{FH}} = \frac{{AC}}{{CH}} \Leftrightarrow AF.CH = FH.AC\)
c) Xét đường tròn \(\left( O \right)\) có \(\widehat {FGC} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn) suy ra \(CG \bot FI\)
Xét tam giác \[IFC\] có \(FD;CG\) là hai đường cao mà \(FD\) cắt \(CG\) tại \(K\) suy ra \(K\) là trực tâm
Suy ra \(IK \bot FC\)
Xét đường tròn \(\left( O \right)\) có \(\widehat {FDA} = \widehat {FCG}\) ( hai góc nội tiếp cùng chắn )
Mà \(\widehat {FDA} = \widehat {BCA}\) ( hai góc nội tiếp cùng chắn )
Do đó \(\widehat {BCA} = \widehat {FCG}\) hay \(\widehat {FCE} = \widehat {FCG}\)
Xét \(\Delta FEC\) và \(\Delta FGC\) có \(\widehat {FCE} = \widehat {FCG}\) và \(\widehat {FEC} = \widehat {FGC} = 90^\circ \)
Suy ra do đó
Xét đường tròn tâm \(\left( O \right)\) có
Suy ra \(\widehat {GFC} = \widehat {EDC}\) hay \(\widehat {IFH} = \widehat {HDC}\)
Xét tứ giác \(FHDI\) có \(\widehat {IFH} = \widehat {HDC}\) mà góc ngoài bằng góc trong đỉnh đối diện nên \(FHDI\) là tứ giác nội tiếp
Suy ra \(\widehat {FHI} = \widehat {FDI} = 90^\circ \Rightarrow IH \bot FC\)
Suy ra \(K;I;H\) thẳng hàng
Lời giải
Gọi d là đường thẳng trong \(2025\) đường thẳng thỏa mãn đề bài
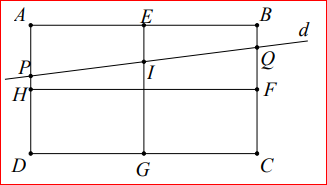
Giả sử d cắt \(AD;BC\) lần lượt tại \(P;Q\) và cắt \(EG\) tại \(I\)
\(E;F;G;H\) là trung điểm các cạnh như hình
Mà \({S_{DCQP}} = 2{S_{ABQP}} \Rightarrow \left( {DP + QC} \right) = 2\left( {AP + BQ} \right) \Leftrightarrow GI = 2IE \Leftrightarrow GI = \frac{2}{3}GE\) suy ra \(I\) cố định
Khi đó ta có \(2025 = 4.506 + 1\) các đường thẳng thỏa mãn đề bài phải đi qua 4 điểm cố định khi đó theo nguyên lý Dirichlet thì có \(506 + 1 = 507\) đường thẳng đi qua một điểm