a)$\left\{ {\begin{array}{*{20}{c}}{x + y = 3}\\{2x - y = 9}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3x = 12}\\{x + y = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 4}\\{y = - 1}\end{array}} \right.} \right.} \right.$

b) ${x^2} + 5x + 4 = 0$

Ta có : $a - b + c = 1 - 5 + 4 = 0$ nên phương trình có 2 nghiệm phân biệt $\left[ {\begin{array}{*{20}{c}}{{x_1} = - 1}\\{{x_2} = - 4}\end{array}} \right.$

Câu 3/6

Cho hàm số $y = - {x^2}$ có đồ thị là parabol $(P)$ và hàm số $y = x - m$ có đồ thị là đường thẳng $(d)$ (với $m$ là tham số).

a) Vẽ đồ thị $(P)$ trên mặt phẳng tọa độ \[Oxy.\]

b) Tìm giá trị của $m$ để đường thẳng $(d)$cắt parabol $(P)$ tại hai điểm phân biệt có hoành độ ${x_1},{x_2}$ sao cho biểu thức $T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2$ đạt giá trị lớn nhất.

Xem đáp án

Lời giải

a) Vẽ đồ thị $(P)$ trên mặt phẳng tọa độ \[Oxy.\]

Bảng giá trị

$x$	-2	-1	0	1	2
$y = - {x^2}$	-4	-1	0	-1	-4

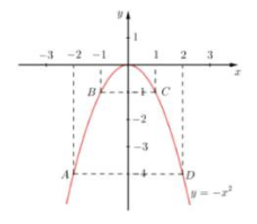
$Cho hàm số $y = - {x^2}$ có đồ thị là parabol $(P)$ và hàm số (ảnh 1)$

b)Phương trình hoành độ giao điểm $ - {x^2} = x - m \Leftrightarrow {x^2} + x - m = 0\,\,(*)$

Đường thẳng (d) cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt

Theo hệ thức Vi-ét ta có: $\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - 1}\\{{x_1}{x_2} = - m}\end{array}} \right.$

Theo đề bài ta có: $T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2$

$\begin{array}{l} = {x_1} + {x_2} - 2{x_1}{x_2} - 2x_1^2x_2^2\\ = - 1 + 2m - 2{m^2}\\ = - 2{\left( {m - \frac{1}{2}} \right)^2} - \frac{1}{2} \le - \frac{1}{2}\forall m\end{array}$

Dấu ‘‘=’’ xảy ra $ \Leftrightarrow m = \frac{1}{2}$ (TMĐK)

Vậy ${T_{\min }} = \frac{{ - 1}}{2}$ khi $m = \frac{1}{2}.$

Câu 4/6

Trong kỳ thi tuyển sinh lớp 10 năm học 2023-2024 của tỉnh Sóc Trăng, bạn An trúng tuyển thủ khoa nên được cha mẹ thưởng cho một chiếc điện thoại mới. Khi đến cửa hàng điện thoại An được tư vấn nếu mua điện thoại kèm phụ kiện thì giá của phụ kiện sẽ được giảm giá 30% so với giá niêm yết ban đầu. Biết rằng tổng giá tiền điện thoại và phụ kiện ban đầu là $11\,500\,000$ đồng và nhờ mua hai thứ nên cha mẹ An chỉ phải trả tổng số tiền là $11\,050\,000$ đồng. Hãy tính giá của chiếc điện thoại mà An được thưởng là bao nhiêu tiền?

Xem đáp án

Lời giải

Gọi giá tiền của chiếc điện thoại mà An được thưởng và giá tiền phụ kiện lần lượt là $x$và $y$ (đồng), $x > 0,y > 0.$

Theo đề bài ta có hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{x + y = 11500000\,\,\,\,\,}\\{x + 0,7y = 11050000}\end{array}} \right.$

Giải hpt ta được $\left\{ {\begin{array}{*{20}{c}}{x = 10000000}\\{y = 1500000}\end{array}} \right.$ (TMĐK)

Vậy giá tiền của chiếc điện thoại mà AN được thưởng là \[10{\rm{ }}000{\rm{ }}000\] đồng.

Câu 5/6

Cho tam giác \[ABC\] vuông tại $A,$ có đường cao $AH$ và $AB = 6cm,$ $AC = 8cm.$ Gọi $N$ là trung điểm của $BC,$ kẻ $NO$ vuông góc với $AC$ tại $O.$

a) Chứng minh $AONH$ là tứ giác nội tiếp.

b) Chứng minh $CO.CA = CN.CH.$
c) Tính độ dài đường cao $NI$ của tam giác $NHO.$

Xem đáp án

Lời giải

$Cho tam giác \[ABC\] vuông tại $A,$ có đường cao $AH$ và $AB = 6cm,$ (ảnh 1)$

a) Chứng minh $AONH$ là tứ giác nội tiếp.

Xét tứ giác AONH có :

$\widehat {AHN} = \widehat {AON} = {90^0}$

$ \Rightarrow \widehat {AHN} + \widehat {AON} = {180^0}$

$ \Rightarrow $Tứ giác AONH là tứ giác nội tiếp.

b) Chứng minh $CO.CA = CN.CH.$

Xét ∆CON và ∆CHA có :

$\widehat {ACH}$ chung

c) Tính độ dài đường cao $NI$ của tam giác $NHO.$

Kẻ $NI \bot OH$ tại I

Xét $\Delta OIN$ và $\Delta AHN$ có :

$\widehat {NOI} = \widehat {NAH}$(cùng chắn )

$\widehat {OIN} = \widehat {AHN} = {90^0}$

Ta có : N là trung điểm của BC (gt)

$\left\{ {\begin{array}{*{20}{c}}{AB \bot AC}\\{ON \bot AC}\end{array}} \right. \Rightarrow ON\parallel AB$

⇒ O là trung điểm của AC

⇒ ON là đường trung bình của tam giác ABC.

$ \Rightarrow ON = \frac{1}{2}AB = \frac{1}{2}.6 = 3(cm).$

Xét tam giác ABC $\left( {\widehat A = {{90}^0}} \right)$, đường cao AH có $BC = 10cm$

$ \Rightarrow BN = \frac{1}{2}BC = 5(cm)$

$\begin{array}{l}AN = \frac{1}{2}BC = 5(cm)\\BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6(cm)\end{array}$

$ \Rightarrow HN = BN - BH = 5 - 3,6 = 1,4(cm)$

Thay độ dài ON, HN, AN vào (*) ta có $NI = \frac{{ON.HN}}{{AN}} = \frac{{3.1,4}}{5} = 0,84(cm).$

Câu 6/6

Một bể cá hình cầu có bán kính bằng $9cm.$ Người ta cần đổ vào bể một lượng nước chiếm $\frac{2}{3}$ thể tích bể. Hỏi cần đổ bao nhiêu lít nước ? (biết rằng $1l = 1000c{m^3},\pi = 3,14)$

Xem đáp án

Lời giải

$Một bể cá hình cầu có bán kính bằng $9cm.$ Người ta cần đổ vào bể một lượng nước chiếm (ảnh 1)$

Thể tích bể cá cảnh là : $\frac{4}{3}\pi {R^3} = \frac{4}{3}.3,{14.9^3} = 3052,08(c{m^3})$

Thể tích lượng nước cần đổ là :$\frac{2}{3}.3052,08 = 2034,72(c{m^3}) = 2,03472$ lít

Vậy người ta cần đổ $2,03472$ lít.

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

\(x\)	-2	-1	0	1	2
\(y = - {x^2}\)	-4	-1	0	-1	-4

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Giải hệ phương trình và phương trình :

a) \(\left\{ {\begin{array}{*{20}{c}}{x + y = 3}\\{2x - y = 9}\end{array};} \right.\) b) \({x^2} + 5x + 4 = 0.\)