Trong kỳ thi tuyển sinh lớp 10 năm học 2023-2024 của tỉnh Sóc Trăng, bạn An trúng tuyển thủ khoa nên được cha mẹ thưởng cho một chiếc điện thoại mới. Khi đến cửa hàng điện thoại An được tư vấn nếu mua điện thoại kèm phụ kiện thì giá của phụ kiện sẽ được giảm giá 30% so với giá niêm yết ban đầu. Biết rằng tổng giá tiền điện thoại và phụ kiện ban đầu là \(11\,500\,000\) đồng và nhờ mua hai thứ nên cha mẹ An chỉ phải trả tổng số tiền là \(11\,050\,000\) đồng. Hãy tính giá của chiếc điện thoại mà An được thưởng là bao nhiêu tiền?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi giá tiền của chiếc điện thoại mà An được thưởng và giá tiền phụ kiện lần lượt là \(x\)và \(y\) (đồng), \(x > 0,y > 0.\)
Theo đề bài ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y = 11500000\,\,\,\,\,}\\{x + 0,7y = 11050000}\end{array}} \right.\)
Giải hpt ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 10000000}\\{y = 1500000}\end{array}} \right.\) (TMĐK)
Vậy giá tiền của chiếc điện thoại mà AN được thưởng là \[10{\rm{ }}000{\rm{ }}000\] đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Thể tích bể cá cảnh là : \(\frac{4}{3}\pi {R^3} = \frac{4}{3}.3,{14.9^3} = 3052,08(c{m^3})\)
Thể tích lượng nước cần đổ là :\(\frac{2}{3}.3052,08 = 2034,72(c{m^3}) = 2,03472\) lít
Vậy người ta cần đổ \(2,03472\) lít.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bảng giá trị
|
\(x\) |
-2 |
-1 |
0 |
1 |
2 |
|
\(y = - {x^2}\) |
-4 |
-1 |
0 |
-1 |
-4 |
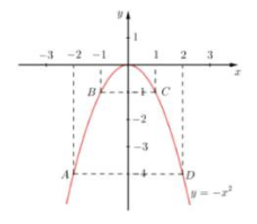
b)Phương trình hoành độ giao điểm \( - {x^2} = x - m \Leftrightarrow {x^2} + x - m = 0\,\,(*)\)
Đường thẳng (d) cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - 1}\\{{x_1}{x_2} = - m}\end{array}} \right.\)
Theo đề bài ta có: \(T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2\)
\(\begin{array}{l} = {x_1} + {x_2} - 2{x_1}{x_2} - 2x_1^2x_2^2\\ = - 1 + 2m - 2{m^2}\\ = - 2{\left( {m - \frac{1}{2}} \right)^2} - \frac{1}{2} \le - \frac{1}{2}\forall m\end{array}\)
Dấu ‘‘=’’ xảy ra \( \Leftrightarrow m = \frac{1}{2}\) (TMĐK)
Vậy \({T_{\min }} = \frac{{ - 1}}{2}\) khi \(m = \frac{1}{2}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập