Rút gọn biểu thức : \[A = \sqrt {25}  + 2\sqrt {27}  - 3\sqrt {12} .\]

a) Vẽ đồ thị \((P)\) trên mặt phẳng tọa độ \[Oxy.\]

Bảng giá trị

\(x\)	-2	-1	0	1	2
\(y =  - {x^2}\)	-4	-1	0	-1	-4

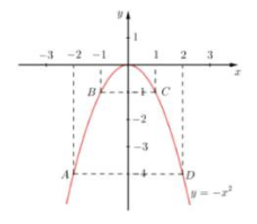
b)Phương trình hoành độ giao điểm \( - {x^2} = x - m \Leftrightarrow {x^2} + x - m = 0\,\,(*)\)

Đường thẳng (d) cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt

Theo hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} =  - 1}\\{{x_1}{x_2} =  - m}\end{array}} \right.\)

Theo đề bài ta có: \(T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2\)

                                  \(\begin{array}{l} = {x_1} + {x_2} - 2{x_1}{x_2} - 2x_1^2x_2^2\\ =  - 1 + 2m - 2{m^2}\\ =  - 2{\left( {m - \frac{1}{2}} \right)^2} - \frac{1}{2} \le  - \frac{1}{2}\forall m\end{array}\)

Dấu ‘‘=’’ xảy ra \( \Leftrightarrow m = \frac{1}{2}\) (TMĐK)

Vậy \({T_{\min }} = \frac{{ - 1}}{2}\) khi \(m = \frac{1}{2}.\)