Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 6
46 người thi tuần này 4.6 280 lượt thi 11 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi khảo sát Toán 9 (chuyên) năm 2026 THPT Chuyên Lê Quý Đôn (TP.HCM) có đáp án
Đề thi thử vào lớp 10 môn Toán (không chuyên) năm 2026 THCS Hậu Giang (TP.HCM) có đáp án
Đề khảo sát Toán 9 năm 2026 Trường THCS Nghĩa Mai (Nghệ An) có đáp án
Đề khảo sát Toán 9 năm 2026 Trường THCS Lý Sơn (Hà Nội) có đáp án
Đề khảo sát Toán 9 năm 2026 Trường THCS Gia Quất (Hà Nội) Tháng 4/2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
Lời giải
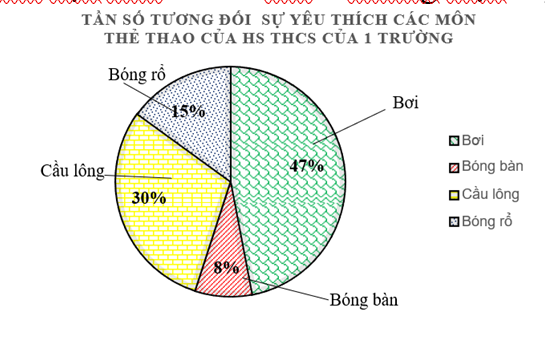
Bảng tần số tương đối của biểu đồ trên là:
|
Môn thể thao được yêu thích |
Bơi |
Bóng bàn |
Cầu lông |
Bóng rổ |
|
Tần số tương đối |
\(47\% \) |
\(8\% \) |
\(30\% \) |
\(15\% \) |
Môn thể thao nào được học sinh THCS của \(1\) trường yêu thích nhất là môn bơi vì môn bơi chiếm \(47\% \) các bạn yêu thích.
Lời giải
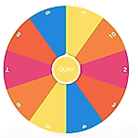
Không gian mẫu của phép thử là
\[\Omega = \left\{ {1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5; \ldots ..;{\rm{ 10}}} \right\}\].
Không gian mẫu có 10 phần tử.
Vì các phần của đĩa tròn giống nhau nên các kết quả của phép thử là đồng khả năng.
Có 4 kết quả thuận lợi cho biến cố A là \[2;\,3;\,5;\,7\]. Xác suất của biến cố A là \(P\left( A \right) = \frac{4}{{10}} = \frac{2}{5}.\)
Đoạn văn 2
Lời giải
Thay \(x = 9\left( {TM} \right)\) vào biểu thức A, ta có:
\(A = \frac{{\sqrt 9 + 5}}{{2\sqrt 9 - 4}} = \frac{{3 + 5}}{{2.3 - 4}} = \frac{8}{2} = 4\)
Vậy \(A = 4\) khi \(x = 9\).
Câu 4/11
Lời giải
\(B = \frac{x}{{x - 4}} + \frac{1}{{\sqrt x - 2}} + \frac{1}{{\sqrt x + 2}}\) với \(x > 0,x \ne 4\).
\(\begin{array}{l}B = \frac{{x + \sqrt x + 2 + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\B = \frac{{x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x }}{{\sqrt x - 2}}\end{array}\)
Lời giải
Ta có \(P = \frac{A}{B} = \frac{{\sqrt x + 5}}{{2\sqrt x - 4}}.\frac{{\sqrt x - 2}}{{\sqrt x }} = \frac{{\sqrt x + 5}}{{2\sqrt x }}\)
Ta có \(P > 1 \Leftrightarrow \frac{{\sqrt x + 5}}{{2\sqrt x }} - 1 > 0 \Leftrightarrow \frac{{5 - \sqrt x }}{{2\sqrt x }} > 0\) mà \(2\sqrt x > 0\) nên \(5 - \sqrt x > 0 \Leftrightarrow x < 25\)
Kết hợp với điều kiện \(x > 0,x \ne 4\) suy ra \(0 < x < 25\), \(x \ne 4\) mà x nguyên lớn nhất suy ra \(x = 24.\)
Vậy \(x = 24\) thì \(P > 1\).
Đoạn văn 3
Lời giải
Gọi số tiền cô Linh đầu tư cho khoản thứ nhất và thứ hai lần lượt là \(x;y\) (triệu đồng, \(0 < x;y < 500\))
Theo đề bài ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 500\\5\% .x + 6\% .y = 28\end{array} \right.\)
Giải được \(\left\{ \begin{array}{l}x = 200\\y = 300\end{array} \right.\left( {tm} \right)\)
Vậy cô Linh đầu tư \(200\) triệu vào khoản thứ nhất và \(300\) triệu vào khoản thứ hai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 5/11 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập