Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Toán Hà Nam có đáp án
38 người thi tuần này 4.6 78 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề KSCL THCS Văn Quán - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Phú Diễn - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Lê Lợi - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Thịnh Quang - HN_năm học 2025-2026_Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bắc Kạn năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Lắk năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Long An năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
|
\(A = \frac{{{{\left( {\sqrt x } \right)}^3} - 1}}{{1 + \sqrt x + x}}.\left[ {\frac{{\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{\sqrt x - 2}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}} \right]\) |
|
\( = \frac{{(\sqrt x - 1)(x + \sqrt x + 1)}}{{1 + \sqrt x + x}}.\left[ {\frac{{\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{\sqrt x - 2}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}} \right]\) |
|
\( = \left( {\sqrt x - 1} \right)\left( {\frac{1}{{\sqrt x - 1}} - \frac{1}{{\sqrt x + 1}}} \right)\) |
|
\( = \left( {\sqrt x - 1} \right)\frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\) |
|
\( = \frac{2}{{\sqrt x + 1}}.\) |
Lời giải
Giả sử số tự nhiên \(n\) thỏa mãn đề bài. Khi đó tồn tại số nguyên dương \(k\) sao cho
\({2^{2024}} + {2^{2027}} + {2^n} = {k^2} \Leftrightarrow {9.2^{2024}} + {2^n} = {k^2} \Leftrightarrow \left( {k + {{3.2}^{1012}}} \right)\left( {k - {{3.2}^{1012}}} \right) = {2^n}\).
\( \Rightarrow \left\{ \begin{array}{l}k + {3.2^{1012}} = {2^a}\\k - {3.2^{1012}} = {2^b}\\a,b \in \mathbb{N},a + b = n\end{array} \right.\)\( \Rightarrow {2^a} - {2^b} = {3.2^{1013}}\) .
\( \Leftrightarrow {2^b}({2^{a - b}} - 1) = {3.2^{1013}} \Leftrightarrow \left\{ \begin{array}{l}{2^{a - b}} - 1 = 3\\{2^b} = {2^{1013}}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a - b = 2\\b = 1013\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1015\\b = 1013\end{array} \right. \Rightarrow n = 2028\)
Vậy với \(n = 2028\)thì \({2^{2024}} + {2^{2027}} + {2^n}\) là số chính phương:
Lời giải
1) \((x - 1)\sqrt {{x^2} + 6x + 16} = 2{x^2} - 6x + 4 \Leftrightarrow (x - 1)\sqrt {{x^2} + 6x + 16} = (x - 1)(2x - 4)\)
\( \Leftrightarrow (x - 1)(\sqrt {{x^2} + 6x + 16} - 2x + 4) = 0\)+)\(\sqrt {{x^2} + 6x + 16} = 2x - 4 \Leftrightarrow \left\{ \begin{array}{l}2x - 4 \ge 0\\{x^2} + 6x + 16 = {(2x - 4)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\3{x^2} - 22x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 0(l)\\x = \frac{{22}}{3}(tm)\end{array} \right.\end{array} \right.\)2) Điều kiện: \(\left\{ \begin{array}{l}3({x^2} + y) + 7 \ge 0\\5{x^2} + 5y + 14 \ge 0\end{array} \right.\)
Phương trình \((1)\) tương đương với
\(\begin{array}{l}\,\,\,\,\,\,2{x^3} + 2x{y^2} - {x^2}y + 2{x^2} + 6x = xy + {y^3} + 3y\\ \Leftrightarrow (2{x^3} - {x^2}y) + (2x{y^2} - {y^3}) + (2{x^2} - xy) + (6x - 3y) = 0\\ \Leftrightarrow {x^2}(2x - y) + {y^2}(2x - y) + x(2x - y) + 3(2x - y) = 0\\ \Leftrightarrow (2x - y)({x^2} + {y^2} + x + 3) = 0\end{array}\)\( \Leftrightarrow (2x - y){\rm{[}}{(x + \frac{1}{2})^2} + {y^2} + \frac{{11}}{4}{\rm{]}} = 0\,\)
\( \Leftrightarrow 2x - y = 0 \Leftrightarrow y = 2x\)Thay \(y = 2x\) vào phương trình \((2)\) ta được
\(\begin{array}{l}\,\,\,\,\,\sqrt {3{x^2} + 6x + 7} + \sqrt {5{x^2} + 10x + 14} = 4 - 2x - {x^2}\\ \Leftrightarrow (\sqrt {3{x^2} + 6x + 7} - 2) + (\sqrt {5{x^2} + 10x + 14} - 3) + ({x^2} + 2x + 1) = 0\\ \Leftrightarrow \frac{{3{{(x + 1)}^2}}}{{\sqrt {3{x^2} + 6x + 7} + 2}} + \frac{{5{{(x + 1)}^2}}}{{\sqrt {5{x^2} + 10x + 14} + 3}} + {(x + 1)^2} = 0\\ \Leftrightarrow {(x + 1)^2}(\frac{3}{{\sqrt {3{x^2} + 6x + 7} + 2}} + \frac{5}{{\sqrt {5{x^2} + 10x + 14} + 3}} + 1) = 0\end{array}\)
Vì \(\frac{3}{{\sqrt {3{x^2} + 6x + 7} + 2}} + \frac{5}{{\sqrt {5{x^2} + 10x + 14} + 3}} + 1 > 0\) nên phương trình tương đương với
\({(x + 1)^2} = 0 \Leftrightarrow x + 1 = 0 \Leftrightarrow x = - 1 \Rightarrow y = - 2\,\,(tm)\)
Vậy hệ phương trình có nghiệm \((x;y) = ( - 1; - 2)\)Lời giải
Câu IV. (4 điểm) Cho đường tròn \(\left( O \right)\) có dây cung \(BC\) cố định và không đi qua tâm \(O\). Gọi \(A\) là điểm di động trên đường tròn \(\left( O \right)\) sao cho tam giác \(ABC\) nhọn và \(AB < AC.\) Gọi \(M\) là trung điểm của cạnh \(BC\) và \(H\) là trực tâm tam giác \(ABC.\) Tia \(MH\) cắt đường tròn \(\left( O \right)\) tại \(K\), đường thẳng \(AH\) cắt cạnh \(BC\) tại \(D\) và \(AE\) là đường kính của đường tròn \(\left( O \right)\) .
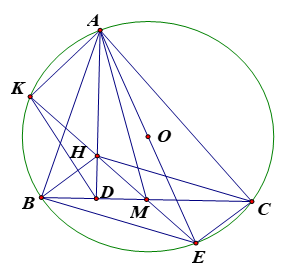
1. ( 1,0 điểm) Chứng minh \(\widehat {BAD} = \widehat {CAE}.\)
\(AH \bot BC \Rightarrow \widehat {ADB} = {90^0}\)
\(\widehat {ABE} = {90^0}\) ( góc nội tiếp chắn nửa đường tròn)
Suy ra \(\widehat {BAD} = \widehat {CBE}\) ( cùng phụ với \(\widehat {ABC}\) )
Mà \(\widehat {CBE} = \widehat {CAE}\) ( góc nội tiếp cùng chắn cung )
Suy ra \(\widehat {BAD} = \widehat {CAE}.\)
2. ( 1,0 điểm) Chứng minh rằng tứ giác \(BHCE\) là hình bình hành và \(HA.HD = HK.HM\).
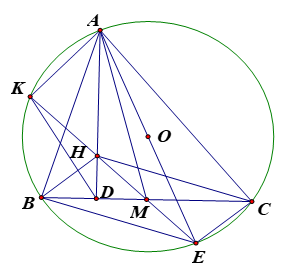
Ta có \(\widehat {ACE} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow EC \bot AC\).
Mà \[H\]là trực tâm tam giác \(ABC\) \( \Rightarrow BH \bot AC\). Từ đó suy ra \(EC\;{\rm{//}}\;BH\).
Tương tự \[HC\;{\rm{//}}\;BE\]
Xét tứ giác \[BHCE\] có \(EC\;{\rm{//}}\;BH\) và \[HC\;{\rm{//}}\;BE\] nên tứ giác \[BHCE\] là hình bình hành.
Mà \(M\) là trung điểm của \[BC\] nên ba điểm \[H,{\rm{ }}M,{\rm{ }}E\] thẳng hàng.
Lại có ba điểm \[M,{\rm{ }}K,{\rm{ }}H\] thẳng hàng. Từ đó suy ra ba điểm \(K,\,H,\,E\) thẳng hàng.
Ta có \(\widehat {AKE} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {AKM} = 90^\circ \).
Xét \(\Delta AKH\) và \(\Delta MDH\) có: \(\widehat {AKM} = \widehat {MDH}\;\left( { = 90^\circ } \right)\); \(\widehat {KHA} = \widehat {DHM}\) (hai góc đối đỉnh).
\( \Rightarrow HA.HD = HK.HM\).
3. ( 1,0 điểm) Tia \(KD\) cắt đường tròn \(\left( O \right)\) tại \(I\) (\(I\) khác \(K\)), đường thẳng đi qua \(I\) và vuông góc với đường thẳng \(BC\) cắt \(AM\) tại \(J\). Chứng minh rằng các đường thẳng \(AK,\,\,BC\) và \(HJ\) cùng đi qua một điểm.
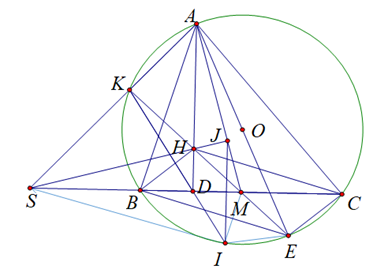
Kéo dài \[AK\] cắt đường thẳng \[BC\] tại \[S\], \(\Delta SAM\) có hai đường cao \(AD\) và \(MK\)cắt nhau tại \(H\)\[ \Rightarrow H\] là trực tâm tam giác \[SAM\].
Xét tam giác \(\Delta HDM\) và \(\Delta SDA\) có \(\widehat {ADS} = \widehat {HDM} = 90^\circ \) và \(\widehat {DMH} = \widehat {DAS}\) (cùng phụ với \(\widehat {ASM}\)).
\( \Rightarrow \frac{{HD}}{{DM}} = \frac{{DS}}{{AD}}\). (1)
Tương tự \[H\] là trực tâm \[\Delta ABC\]. (2)
Từ (1) và (2) \( \Rightarrow \frac{{HD}}{{DM}}.\frac{{BD}}{{HD}} = \frac{{DS}}{{AD}}.\frac{{AD}}{{CD}} \Rightarrow \frac{{BD}}{{DM}} = \frac{{DS}}{{CD}} \Rightarrow BD.CD = DM.DS\) (3)
Mà \( \Rightarrow \frac{{BD}}{{ID}} = \frac{{DK}}{{DC}}\,\, \Rightarrow BD.CD = DI.DK\) (4)
Từ (3) và (4)\( \Rightarrow DI.DK = DM.DS\) nên \[SKMI\] là tứ giác nội tiếp \( \Rightarrow \widehat {SMI} = \widehat {SKI}\).
Mà \(AKDM\) là tứ giác nội tiếp (do \(\widehat {AKM} = \widehat {ADM} = 90^\circ \)) \( \Rightarrow \widehat {SKI} = \widehat {DMA}\).
Từ đó suy ra \(\widehat {SMI} = \widehat {DMA}\).
Xét \(\Delta MIJ\) có \(\widehat {SMI} = \widehat {DMA}\) và \(IJ \bot BC\)\( \Rightarrow BC\) là đường trung trực của \[IJ\].
\[ \Rightarrow \widehat {SJM} = \widehat {SIM} = 90^\circ \] (vì \[SKMI\] là tứ giác nội tiếp nên \(\widehat {SIM} = 180^\circ - \widehat {SKM}\) \( = 180^\circ - 90^\circ = 90^\circ \)) \( \Rightarrow SJ \bot AM\).
Mà \[H\] là trực tâm \[\Delta SAM\]\( \Rightarrow SH \bot AM\). Từ đó suy ra ba điểm \(S,\,\,H,\,\,J\) thẳng hàng. Vậy các đường thẳng \(AK,\,\,BC\) và \(HJ\) cùng đi qua điểm \(S\).
4.(1,0 điểm) Một đường tròn thay đổi luôn tiếp xúc với \(AK\) tại \(A\) và cắt các cạnh \(AB,\,\,AC\) lần lượt tại \(P,\,\,Q\) phân biệt. Gọi \(N\) là trung điểm của đoạn thẳng \(PQ\). Chứng minh rằng đường thẳng\(AN\) luôn đi qua một điểm cố định.
\(\Delta BEM\)
Gọi \[N'\] là giao điểm của \[PQ\] và \[AE.\] Xét \(\Delta AQN'\) và \(\Delta BEM\) có:
\(\widehat {QAN'} = \widehat {EBM}\); \(\widehat {AQN'} = \widehat {KAP} = \widehat {BEM}\)
(5)
Do \(\widehat {QAN'} = \widehat {EBM}\); \(\widehat {AQN'} = \widehat {KAP} = \widehat {BEM}\) nên theo tính chất góc ngoài của \(\Delta AQN'\) và ta có \(\widehat {EMC} = \widehat {PN'A}\).
Mà \(\widehat {PAN'} = \widehat {ECM}\) nên \( \Rightarrow \frac{{CM}}{{EM}} = \frac{{AN'}}{{PN'}}\). (6)
Từ (5) và (6) và kết hợp \(BM = CM\)\( \Rightarrow \frac{{AN'}}{{QN'}} = \frac{{AN'}}{{PN'}} \Rightarrow QN' = PN' \Rightarrow N \equiv N'\).
Vậy \(AN\) luôn đi qua một điểm cố định \(O\).
Lời giải
Với \(a,b,c > 0\), chứng minh được:
Với \(a,b > 0\), ta có :
\(\begin{array}{l}5{a^2} + 2ab + 2{b^2} = (4{a^2} + 4ab + {b^2}) + ({a^2} - 2ab + {b^2})\\ = {(2a + b)^2} + {(a - b)^2} \ge {(2a + b)^2}\\ \Rightarrow \sqrt {5{a^2} + 2ab + 2{b^2}} \ge \sqrt {{{(2a + b)}^2}} = 2a + b\end{array}\):
\( \Rightarrow \frac{1}{{\sqrt {5{a^2} + 2ab + 2{b^2}} }} \le \frac{1}{{2a + b}} \le \frac{1}{9}\left( {\frac{1}{a} + \frac{1}{a} + \frac{1}{b}} \right) = \frac{1}{9}\left( {\frac{2}{a} + \frac{1}{b}} \right)\)
Tương tự: \(\frac{1}{{\sqrt {5{b^2} + 2bc + 2{c^2}} }} \le \frac{1}{9}\left( {\frac{2}{b} + \frac{1}{c}} \right){\rm{ ; }}\frac{1}{{\sqrt {5{c^2} + 2ca + 2{a^2}} }} \le \frac{1}{9}\left( {\frac{2}{c} + \frac{1}{a}} \right)\):
\(P \le \frac{1}{9}\left( {\frac{2}{a} + \frac{1}{b} + \frac{2}{b} + \frac{1}{c} + \frac{2}{c} + \frac{1}{a}} \right) = \frac{1}{3}\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \Rightarrow P \le \frac{1}{3} \cdot \sqrt {3\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)} = \frac{1}{3} \cdot \sqrt 3 = \frac{{\sqrt 3 }}{3}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = 1\end{array} \right. \Leftrightarrow a = b = c = \sqrt 3 \)
Vậy \(\max P = \frac{{\sqrt 3 }}{3}\) khi \(a = b = c = \sqrt 3 \).: