Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 47

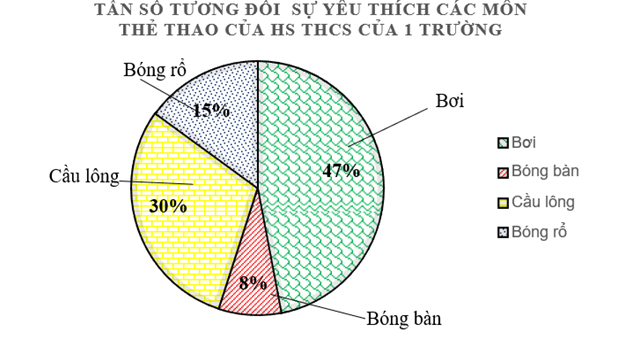
a) Bảng tần số tương đối của biểu đồ trên là:                    

b) Môn thể thao nào được học sinh THCS của \(1\) trường yêu thích nhất là môn bơi vì môn bơi chiếm \(47\% \) các bạn yêu thích.

a. Không gian mẫu của phép thử là:

.

Không gian mẫu có \[{\rm{6}}\]phần tử.

b. Vì các viên bi có cùng kích thước và khối lượng nên các kết quả là đồng khả năng.

+ Có \[{\rm{2}}\] kết quả thuận lợi cho biến cố \[{\rm{A}}\] là: .

Xác suất của biến cố \[{\rm{A}}\]là \(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\).

+ Có \[3\] kết quả thuận lợi cho biến cố \[{\rm{B}}\] là: .

 Xác suất của biến cố \[{\rm{B}}\] là \(P\left( B \right) = \frac{3}{6} = \frac{1}{2}\).

+ Có \[{\rm{4}}\] kết quả thuận lợi cho biến cố \[{\rm{C}}\] là: .

 Xác suất của biến cố \[{\rm{C}}\] là \(P\left( C \right) = \frac{4}{6} = \frac{2}{3}\).

a) Thay \[x = 25\](thỏa mãn điều kiện) vào biểu thức \[B\] ta được \(B = \frac{1}{{\sqrt {25}  + 2}} = \frac{1}{7}\)

b) \(M = \frac{A}{B}\)

\[M = \left( {\frac{{x + 2}}{{x + \sqrt x  - 2}} - \frac{{2\sqrt x }}{{\sqrt x  - 1}} + \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}} \right):\frac{1}{{\sqrt x  + 2}}\]

\[ = \left( {\frac{{x + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{2\sqrt x }}{{\sqrt x  - 1}} + \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}} \right).\frac{{\sqrt x  + 2}}{1}\]

\[ = \left( {\frac{{\left( {x + 2} \right) - 2\sqrt x \left( {\sqrt x  + 2} \right) + \left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}} \right).\frac{{\sqrt x  + 2}}{1}\]

\[ = \frac{{x + 2 - 2x - 4\sqrt x  + x - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  + 2}}{1}\]

\[ = \frac{{ - 4\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  + 2}}{1} = \frac{{ - 4\sqrt x  + 1}}{{\sqrt x  - 1}}\]

c) Theo đề bài ta có:

\[{M^2} - M = 2\]

\[\left( {M + 1} \right)\left( {M - 2} \right) = 0\]

\[M =  - 1\] hoặc \[M = 2\]

* Với \[{\rm{M =   -  1}}\] ta có \(\frac{{ - 4\sqrt x  + 1}}{{\sqrt x  - 1}} =  - 1\)

\( - 4\sqrt x  + 1 =  - \sqrt x  + 1\)

\(x = 0\) (TMĐK)

* Với \[{\rm{M =  2}}\] ta có \(\frac{{ - 4\sqrt x  + 1}}{{\sqrt x  - 1}} = 2\)

\( - 4\sqrt x  + 1 = 2\sqrt x  - 2\)

\(x = \frac{1}{4}\) (TMĐK)

Với \(x,y,z \ge 0\)

Ta đi chứng minh: \({x^3} + {y^3} + {z^3} \ge 3xyz\)

\({x^3} + 3{x^2}y + 3x{y^2} + {y^3} - 3{x^2}y - 3x{y^2} + {z^3} - 3xyz \ge 0\)

\({\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz \ge 0\)

\({\left( {x + y} \right)^3} + {z^3} - 3xy\left( {x + y} \right) - 3xyz \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x + y} \right)}^2} - \left( {x + y} \right)z + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + 2xy + {y^2} - xz - yz + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} + 2xy + {y^2} - xz - yz + {z^2} - 3xy} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right) \ge 0\)

\(2\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {2{x^2} + 2{y^2} + 2{z^2} - 2xy - 2xz - 2yz} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} - 2xy + {y^2} + {x^2} - 2xz + {z^2} + {y^2} - 2yz + {z^2}} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x - y} \right)}^2} + {{\left( {x - z} \right)}^2} + {{\left( {y - z} \right)}^2}} \right] \ge 0\) (Luôn đúng với mọi \(x,y,z \ge 0\))

Vậy nên \({x^3} + {y^3} + {z^3} \ge 3xyz\)

 Gọi cạnh hình vuông nhỏ là \(x(m,0 < x < 1)\)

Chiều cao của hình hộp là \(x\) (m) 

Chiều dài, chiều rộng của hộp hình hộp là \(1 - 2x\) (m)

Thể tích của hộp hình lập phương khi đó là:  \(({m^3})\)

\(x.(1 - 2x)(1 - 2x)\)\( = \frac{1}{4}.4x.(1 - 2x)(1 - 2x)\)

Áp dụng bất đẳng thức Cauchy ta có:

\(4x.(1 - 2x)(1 - 2x) \le {\left( {\frac{{4x + 1 - 2x + 1 - 2x}}{3}} \right)^3}\)

\(\frac{1}{4}.4x.(1 - 2x)(1 - 2x) \le \frac{1}{4}{\left( {\frac{{4x + 1 - 2x + 1 - 2x}}{3}} \right)^3}\)

\(\frac{1}{4}.4x.(1 - 2x)(1 - 2x) \le \frac{1}{4}.{\left( {\frac{2}{3}} \right)^3} = \frac{2}{{27}}\)

Dấu bằng xảy ra khi \[4x = 1 - 2x\]

\[6x = 1\]

\(x = \frac{1}{6}(TM)\)

Gọi dân số nội thành và ngoại thành lần lượt là \[{\rm{a}}{\rm{,}}\;{\rm{b}}\](\[0 < a,b < 420\], nghìn người)

Ta có: dân số của một tỉnh hay tổng của \[{\rm{a}}\] và \[{\rm{b}}\]là \[{\rm{420}}\] nghìn người nên \[a + b = 420\]

Dân số nội thành là: \[100,8\% a{\rm{ }} = {\rm{ }}1,008a\](người)

Dân số ngoại thành là: \[101,1\% b{\rm{ }} = {\rm{ }}1,011b\](người)

Vì sau một năm dân số toàn tỉnh sẽ tăng 1% nên ta có pt:

\[1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}420{\rm{ }}.101\% \]

\[1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}424,2\]

Ta có hệ phương trình: \[\left\{ \begin{array}{l}a + b = 420\\1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}424,2\end{array} \right.\]

Giải hệ phương trình ta được: \[a = 140;{\rm{ }}b = 280\] 

Vậy dân số nội thành là \[{\rm{140}}\] nghìn người, dân số ngoại thành là \[{\rm{280}}\] nghìn người.

Gọi vận tốc lúc đầu của ô tô là \[x\left( {{\rm{km/h}}} \right){\rm{ }}\left( {x > 0} \right)\]

Vận tốc lúc sau của ô tô là \[{\rm{x + 10}}\]\[\left( {{\rm{km/h}}} \right)\]

Thời gian ô tô đi trên đoạn đường đầu \(\frac{{180}}{x}\) (giờ)

Thời gian ô tô đi trên đoạn đường sau \(\frac{{220}}{{x + 10}}\)(giờ)

Theo đề bài, thời gian ô tô đi trên cả quãng đường là \[{\rm{8}}\] giờ.

Ta có phương trình: \(\frac{{180}}{x} + \frac{{220}}{{x + 10}} = 8\)

Giải phương trình tìm được hai nghiệm: \[{\rm{45}}\] và \[{\rm{ - 5}}\]

Giá trị \(x = 45\) (TMĐK), trả lời.