(1,5 điểm)

Biểu đồ hình quạt tròn dưới đây biểu diễn tần số tương đối của các môn thể thao được yêu thích của học sinh THCS của \(1\) trường hiện nay:  

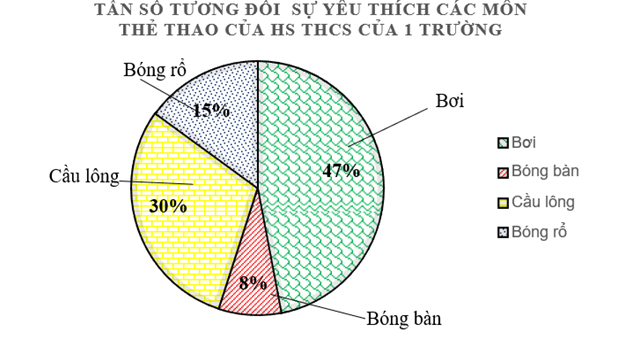
a) Hãy lập bảng tần số tương đối của biểu đồ trên.

b) Môn thể thao nào được học sinh THCS của \(1\) trường yêu thích nhất? Vì sao?

 

Gọi dân số nội thành và ngoại thành lần lượt là \[{\rm{a}}{\rm{,}}\;{\rm{b}}\](\[0 < a,b < 420\], nghìn người)

Ta có: dân số của một tỉnh hay tổng của \[{\rm{a}}\] và \[{\rm{b}}\]là \[{\rm{420}}\] nghìn người nên \[a + b = 420\]

Dân số nội thành là: \[100,8\% a{\rm{ }} = {\rm{ }}1,008a\](người)

Dân số ngoại thành là: \[101,1\% b{\rm{ }} = {\rm{ }}1,011b\](người)

Vì sau một năm dân số toàn tỉnh sẽ tăng 1% nên ta có pt:

\[1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}420{\rm{ }}.101\% \]

\[1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}424,2\]

Ta có hệ phương trình: \[\left\{ \begin{array}{l}a + b = 420\\1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}424,2\end{array} \right.\]

Giải hệ phương trình ta được: \[a = 140;{\rm{ }}b = 280\] 

Vậy dân số nội thành là \[{\rm{140}}\] nghìn người, dân số ngoại thành là \[{\rm{280}}\] nghìn người.

Với \(x,y,z \ge 0\)

Ta đi chứng minh: \({x^3} + {y^3} + {z^3} \ge 3xyz\)

\({x^3} + 3{x^2}y + 3x{y^2} + {y^3} - 3{x^2}y - 3x{y^2} + {z^3} - 3xyz \ge 0\)

\({\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz \ge 0\)

\({\left( {x + y} \right)^3} + {z^3} - 3xy\left( {x + y} \right) - 3xyz \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x + y} \right)}^2} - \left( {x + y} \right)z + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + 2xy + {y^2} - xz - yz + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} + 2xy + {y^2} - xz - yz + {z^2} - 3xy} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right) \ge 0\)

\(2\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {2{x^2} + 2{y^2} + 2{z^2} - 2xy - 2xz - 2yz} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} - 2xy + {y^2} + {x^2} - 2xz + {z^2} + {y^2} - 2yz + {z^2}} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x - y} \right)}^2} + {{\left( {x - z} \right)}^2} + {{\left( {y - z} \right)}^2}} \right] \ge 0\) (Luôn đúng với mọi \(x,y,z \ge 0\))

Vậy nên \({x^3} + {y^3} + {z^3} \ge 3xyz\)

 Gọi cạnh hình vuông nhỏ là \(x(m,0 < x < 1)\)

Chiều cao của hình hộp là \(x\) (m) 

Chiều dài, chiều rộng của hộp hình hộp là \(1 - 2x\) (m)

Thể tích của hộp hình lập phương khi đó là:  \(({m^3})\)

\(x.(1 - 2x)(1 - 2x)\)\( = \frac{1}{4}.4x.(1 - 2x)(1 - 2x)\)

Áp dụng bất đẳng thức Cauchy ta có:

\(4x.(1 - 2x)(1 - 2x) \le {\left( {\frac{{4x + 1 - 2x + 1 - 2x}}{3}} \right)^3}\)

\(\frac{1}{4}.4x.(1 - 2x)(1 - 2x) \le \frac{1}{4}{\left( {\frac{{4x + 1 - 2x + 1 - 2x}}{3}} \right)^3}\)

\(\frac{1}{4}.4x.(1 - 2x)(1 - 2x) \le \frac{1}{4}.{\left( {\frac{2}{3}} \right)^3} = \frac{2}{{27}}\)

Dấu bằng xảy ra khi \[4x = 1 - 2x\]

\[6x = 1\]

\(x = \frac{1}{6}(TM)\)